Engineering Properties of Biological Materials and Food Quality 3(2+1)

Lesson 5. Basics of Thermal properties

5.1. Modes of heat transfer: Conduction Convection Radiation

Fig. 5.1 Modes of heat transfer

When heating and cooling of materials involves unsteady state or transient heat conduction, the material temperature changes with time and knowledge of the thermal diffusivity is required for predicting temperature in these processes.

The interface heat and mass transfer coefficients are important in the design of food processes and processing equipment, and in the control of food packaging and storage. Heat transfer coefficients are essential in thermal processing, in cooling or freezing and in storage operations. Mass transfer coefficients are important in drying and storage of foods, and in separation processes. One basic feature of both coefficients is that they are affected strongly by the characteristics of the processing equipment and the geometry of the system.

Conduction:- Heat transfer from one part of the homogenous opaque solid to another, under influence of the temperature gradient (transfer of heat by direct contact of particles of matter).

• Heat is transfer by conduction when adjacent atoms brush against another or electron moves from one atom to another.

• Steady state amount of heat in heat out = unsteady state.

Convection:- transfer of thermal energy by the movement of molecules from one part of the material to another.

• Material convection

• Forced convection

Radiation:- transfer of heat energy through empty space.

All object with a temperature above absolute zero radiate energy. No medium is necessary, for it is transferred through electromagnetic waves.

Related Physical Properties:-

Space, size, volume, unit surface area, roundness sphericity average projected area are need to be defined as quantified before heat transfer problems involving biological problems can be solved.

For example heat transfer through slab is different than that of sphere.

Specific heat:-

Heat required to raise the temperature by 1^°C for unit mass of the body.

C =\[{q\over{m\Delta T}}\]    q= heat, kcal
C = kcal/ kg^°C   m= mass, kg

\[\Delta\]T= temperature difference, ^°C

Thermal Conductivity:-

Thermal conductivity is defined as the amount of heat flows through unit thickness of material over an unit area per unit time for temperature difference.

 Q=-k\[{{A\left({T1-T2}\right)}\over x}\times t\]
Ability to conduct heat: q= kA\[{{dt}\over{dx}}\]
Thermal conductivity is the quantity heat that passes through a body (plate) of particular area & thickness when it’s opposite faces difference in temperature.
q = kA\[{{dt}\over{dx}}\]  t= Time, dT= temperature difference, dx= thickness
\[{{dQ}\over{d\theta}}\]= kA\[{{dt} \over{dx}}\]  A= Surface area, k= thermal conductivity.

Heat transfer from higher to lower so (dT) accounts for the negativity (So final temperature will have lower value then the initial) to negate that (-) sign. The final equation for

‘k’=\[{{kcal-m}\over{m-hrk}}\] or

Thermal diffusivity:-

It is rate at which heat is diffused out of the materials. It is the ratio between thermal conductivity to volumetric heat capacity.

\[\alpha=\]m²/s=\[\alpha={k\over{PCp}}\]=             PC_p=Volumetric heat capacity

\[{{dt}\over{d\theta}}=\alpha\left({{{d2t}\over{dx2}}+{{d2t}\over{dy2}}+{{d2t}\over{dz2}}}\right)\]

Thermal Emissivity(E):-

It is a ratio of total Emissive power of a blackbody to the same temperature.

This thermal constant is associated with the rate of heat transfer by radiation from a hot body to a cold body.

Q = AF_aF_{e\[\sigma\](T1⁴-T2⁴) E = 1 black body   FaFe<1 real object}

A= surface area

F_a = Angle factor, representing the angle that one body sees the other body.

F_e = Emissivity factor

\[\sigma\]= Stefan Boltzmann constant

T₁ &T₂ = Absolute temperature of body 1 and 2, respectively

While dealing with grey body Kirchhoff’s law of thermal radiation is applied emissivity equals to absorptivity (for an object in thermal equilibrium) so that the body does not absorb all incident light will also emit less radiation then ideal blackbody.

Stefan Boltzmann’s law:- The total energy radiated per unit surface area of a black body is unit time in proportional to the fourth power of the thermodynamic temperature.

 \[\sigma\]=5.670410-⁸ W/ m²k^-4

\[{P\over A}=\]\[\sigma\]T⁴                 J/ m²s    ____Stefan Boltzmann law

\[{P\over A}=E\[\sigma\]T⁴                           T_c = Colder temperature  

P = E\[\sigma\](T⁴ – T_c⁴)                   E= Emissivity

Thermal Effusively:- Square root of the product of the materials thermal conductivity & Volumetric heat capacity.
e = (K_pC_p)^1/2                              K= thermal conductivity

\[{{kal} \over {m2k\root {} \of {hr} }}\]  \[\sqrt{{{kal}\over{S.m.c}}\times{{mg}\over{m^3}}\times{{kal}\over{kg^\circ C}}}\]    p = density, C_p= rp heat

A material thermal effusivity is a measure of its ability to exchange thermal energy with its surrounding.

If two semi-infinite bodies initially at temperature T & T2 are brought in perfect thermal contact, the temperature of the contact surface T_m will be given by their relative thermal effusivity.

T_m= T₁+(T₂-T₁)\[{{{\rm{e}}_{\rm{2}}}\over{\left({{\rm{e}}_{\rm{2}}+{\rm{e}}_{\rm{1}}}\right)}}\]  (For semi infinite bodies in perfect thermal contact)

Diffusivity or diffusion constant is the proportionally constant between the molar flax due to molecular diffusion and the concentration gradient of the sphere.

Through Fick’s law (m²s^-1)

Temperature dependence of the diffusion co-efficient
J =-D\[{{d\theta}\over{de}}\]\[\theta\]=Concentration gradient
-D  W_w= flow rate, A= surface area, y = Any position

D= diffusion Coefficient\[{{dc_W}\over{dy}}=\]change in cold water m²/s

Temperature Dependence

D=\[D_0e{{- E_a}\over{RT}}\]  Arrhenius equation

D_o = maximum diffusion coefficient at infinite temp.

E_a = activation energy

T = Absolute temp, K

R = universal gas constant

Thermal diffusivity is determines the speed of heat of the 3- dimensional propagation or diffusion through the material.

Mass transfer coefficient:-

It is the ratio of mass there of vapour (w_w/A) at any point between the wet and dry surfaces to the difference in concentration of two boundary layers(lw₀-lw_c) between which mass is being transferred.                    

Kc=mass transfer coefficient,

Kc=\[{{n_A }\over{A\Delta c_A^{}}}\] \[\Delta c_A^{}\]=Conc. difference driving force, myl /m³

A=effective man transfer area, m², n_A=man transfer rate(mol / s)

Kc=
This is an analogy with heat transfer coefficient

Coefficient of Thermal expansion:-  The change in size with temperature / C⁰

\[\alpha _V=\left({{1\over V}}\right)\left({{{dV}\over{dT}}}\right)\]V=Volumeofmaterial,\[{{dV}\over{dT}}\]=Rate of volume with temp.
\[{{\Delta T}\over V}=\alpha _VdT\]\[\alpha _V\]=Volumetric thermal expansion

Linear thermal expansion

\[\alpha _L={1\over L}{{dL}\over{dT}}\]
\[{{\Delta L}\over L}=\alpha _L LT\]
\[\alpha _V=3\alpha _L\]
\[\left({V+\Delta V}\right) =\left({L+\Delta L}\right)^3=L^3+3L^2\Delta L+3L\Delta L^2+\Delta L^2\L^3+3L^2\Delta\]
                                           =\[V+3V{{dL}\over L}L^3+L^3\alpha _V\Delta T\]
                                           =\[L^3+3L^3\alpha _L\Delta T+3L^3\alpha _L ^2\Delta T^2+L^3\alpha _L ^3\L^3 3L^3\alpha _L \Delta T\]

Since\[\Delta T\]is small the higher terms can be neglected.

\[\alpha _A={1\over A}{{dA}\over{dT}}\]
\[{{\Delta A}\over A}=\alpha _A \Delta T\]5

Table 5.1 dimensionless number used for calculation of thermal properties

Name	Symbol	Group of Physical properties
Biot member	Bi		H=film heat coefficient  or Convective heat
Fourier number	F0		Transfer coefficient
Levies number	Le()		Lc= characteristic length
Nusselt Number	Nu		K=Thermal conductivity of the  body
Prandlt number	Pr		Α=Thermal Diffusivity
Regnolds number	Rc		=length though which conduction occurs
Schmidt number	Sc		D= Man diffusivity
Stanton number	St

Sc=\[{V\over D} = {\mu\over{PD}}\]

V= kinematic viscosity

\[\eta\left(\mu\right) = dynamicvis\cos ity\]

P= density

\[\Pr = {v \over \alpha } = {{\mu C_p }\over k}\]

C_p= specific heat

v= velocity

Nu=\[{{hL}\over{ks}}\]
St=\[{h\over{c_p pv}}\]   h= convective heat transfer coefficient, P= density of fluid

St=\[{{Nu}\over{R_e .P_r }}\]   C_p= sp heat, v= velocity of the fluid

Specific Heat calculation

C_avg=    C_ps= Sp. Heat of solid not Fat, C_pw= Sp. Heat of water

C_pw = 4186.8M, C_ps=837.36

C_avg= 4186.8M+(1-M)837.36

C_avg=3349M+837.36  J /(ag.k)………….(1)

C_{pf =}  Sp heat of fat = 1676.72

C_avg = 1674.72F + 7.36SNF + 4186.8M (J/ng⁰)………(2)

 Energy Balances

C_p(above freezing point)=\[{{4.19M} \over {110}} + {{0.84(100 - M)} \over {110}}..........kJ/kg^o C\]
C_p(above freezing point)=\[{{2.1M} \over {110}} + {{0.84(100 - M)} \over {110}}\]
                                     =\[335 \times {m \over {100}}\],
K =\[{{0.55M} \over {100}} + {{0.26(100 - M)} \over {100}}\]
Ku/Ou= \[{{2.4M} \over {100}} + {{0.26()100 - M} \over {100}}\]

The thermal properties of food materials depend on the composition of the food. Since most foods are composite of many macro and micromolecules, the thermal properties vary with the composition type. So the properties of food would vary than that of the individual pure molecules. In this context boiling point rise and freezing point depression of the foods are discussed in the following section.

Boiling point Rise:- In liquid food boiling point rise refers to water evaporation in which water change from the liquid phase to steam or vapour phase, and water vapour pressure equals  to the external pre liquid foods contain high molecules  weight  solids that cause the boiling point be evaluated above that of pane water. The boiling point rise (\[\Delta T_r\]), is known as the increase in the boiling point over that of pure water in a given liquid food. As the vapour pressure of most aqueous solution is lower than that of water at the same temperature, the boiling temp(point) of the solution in higher  than that of pure water.

Freezing point Depression: During freezing water in the food changes to ice which heat in removed by a refrigeration system. During heat removal, the unfrozen water will still contain dissolved solids. The presence of dissolved solids will depress the initial freezing point to certain amount \[\Delta Tf\] below the expected solidification temperature of pure water. Freezing point depression is defined as the temperature reduction \[\Delta Tf\].

Both the boiling point rise and freezing point depression of a food are related to its solution concentration.

 

Eutectic point:-  Temperature where there no further concentration  due to freezing , thus the solution frees. Temperature at which a crystal it indecision solute exists in equilibrium with unfrozen liquid rice. Crystallization occurs   below eutectic point. The solution becomes super saturated.

 A eutectic or eutectic mixture is a mixture of two or more phases at a composition that has lowest melting points & where the phases simultaneously crystallize from molten solution at this temperature. The proper ratios of phases to obtain a eutectic identified by the eutectic point on a phase diagram.

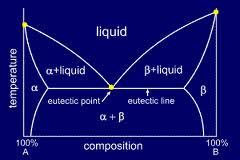
 Fig. Eutectic point in a phase diagram

Frozen foods being thawed for are subjected to quality loss, if thawing is slow. Most concentrated solution that are last to freeze and slow to thaw, since they are eutectic mixture. The eutectic mixture is a solution of such composition that it frozen thaws as separation of pure ice. The frozen eutectic has a constant properties of ice crystal intermingled with solution crystal. The temperature at which a eutectic mixture is formed is called eutectic point or eutectic temperature. Freeze drying should be concerned out at this point. Maximum crystals formations is not possible until this temperature reached

 Table 5.2 the eutectic point of different commodities                        

commodity	Eutectic Temperature
Ice cream	55°C
Meat	50-60°C
Bread	70°C

Application :

Freeze drying:- If eutectic point is not reached quickly the food have pure texture.

Thermal imaging: Infrared imaging for food quality determination

 

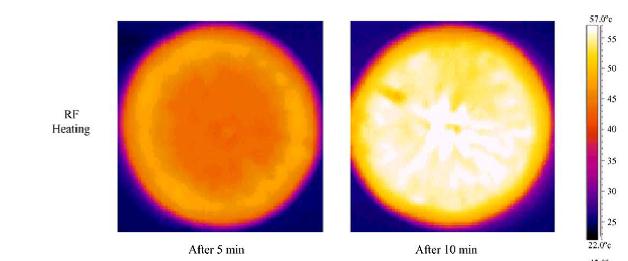
Fig. Thermal imaging of oranges when heated with radio frequency heating system (source: Birla et al., 2004)

References:

• Fundamentals of food process engineering 3^rd equation edited by Romeo T. Toledo, Springer.

• S.L. Birla, S. Wang, J. Tang, G. Hallman. Improving heating uniformity of fresh fruit in radio frequency treatments for pest control. Postharvest Biology and Technology 33 (2004) 205–217