Engineering Physics 3(2+1)

LESSON 12. Qualitative Explanation of Stark Effect

Overview

An electric field pointing from left to right, for example, tends to pull nuclei to the right and electrons to the left.

In another way of viewing it, if an electronic state has its electron disproportionately to the left, its energy is lowered, while if it has the electron disproportionately to the right, its energy is raised.

Other things equal, the effect of the electric field is greater for outer electron shells, because the electron is more distant from the nucleus, so it travels farther left and farther right.

The Stark effect can lead to splitting of degenerate energy levels. For example, in the Bohr model, an electron has the same energy whether it is in the 2s state or any of the 2p states. However, in an electric field, there will be hybrid orbital (also called quantum superposition) of the 2s and 2p states where the electron tends to be to the left, which will acquire a lower energy, and other hybrid orbital where the electron tends to be to the right, which will acquire a higher energy. Therefore, the formerly degenerate energy levels will split into slightly lower and slightly higher energy levels.

Classical electrostatics

The Stark effect originates from the interaction between a charge distribution (atom or molecule) and an external electric field. Before turning to quantum mechanics we describe the interaction classically and consider a continuous charge distribution ρ(r). If this charge distribution is non-polarizable its interaction energy with an external electrostatic potential V(r) is

If the electric field is of macroscopic origin and the charge distribution is microscopic, it is reasonable to assume that the electric field is uniform over the charge distribution. That is, V is given by a two-term Taylor expansion,

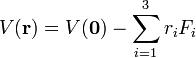, with the electric field: ,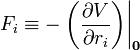

where we took the origin 0 somewhere within ρ. Setting V(0) as the zero energy, the interaction becomes

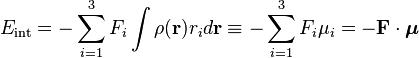
Here we have introduced the dipole moment μ of ρ as an integral over the charge distribution. In case ρ consists of N point charges qj this definition becomes a sum

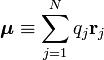
Perturbation theory

Turning now to quantum mechanics we see an atom or a molecule as a collection of point charges (electrons and nuclei), so that the second definition of the dipole applies. The interaction of atom or molecule with a uniform external field is described by the operator

This operator is used as a perturbation in first- and second-order perturbation theory to account for the first- and second-order Stark effect.

First order

Let the unperturbed atom or molecule is in a g-fold degenerate state with ortho- normal 0th -order state functions. (Non-degeneracy is the special case g = 1). According to perturbation theory the first-order energies are the Eigen values of the g x g matrix with general element

If g = 1 (as is often the case for electronic states of molecules) the first-order energy becomes proportional to the expectation (average) value of the dipole operator,

Because a dipole moment is a polar vector, the diagonal elements of the perturbation matrix Vint vanish for systems with an inversion center (such as atoms). Molecules with an inversion center in a non-degenerate electronic state do not have a (permanent) dipole and hence do not show a linear Stark effect.

In order to obtain a non-zero matrix Vint for systems with an inversion center it is necessary that some of the unperturbed functions  have opposite parity (obtain plus and minus under inversion), because only functions of opposite parity give non-vanishing matrix elements. Degenerate 0th -order states of opposite parity occur for excited hydrogen-like (one-electron) atoms. Such atoms have the principal quantum number n among their quantum numbers. The excited state of hydrogen-like atoms with principal quantum number n is n2-fold degenerate and

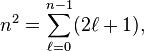
Here   is the angular momentum quantum number

For instance, the excited n = 4 state contains the following  states,

The one-electron states with even are even under parity, while those with odd are odd under parity. Hence, hydrogen-like atom with n>1 shows first-order Stark effect.

The first-order Stark effect occurs in rotational transitions of symmetric top molecules (but not for linear and asymmetric molecules). In first approximation a molecule may be seen as a rigid rotor. A symmetric top rigid rotor has the unperturbed Eigen states

With 2(2J+1)-fold degenerate energy for |K| > 0 and (2J+1)-fold degenerate energy for K=0. Here DJMK is an element of the Wigner D-matrix. The first-order perturbation matrix on basis of the unperturbed rigid rotor function is non-zero and can be diagonalized. This gives shifts and splitting in the rotational spectrum. Quantitative analysis of these Stark shift yields the permanent electric dipole moment of the symmetric top molecule.

Second order

As stated, the quadratic Stark effect is described by second-order perturbation theory. The 0^th -order problems

are assumed to be solved. It is usual to assume that the 0^th -order state to be perturbed is non-degenerate. If we take the ground state as the non-degenerate state under consideration (for hydrogen-like atoms: n = 1), perturbation theory gives

 

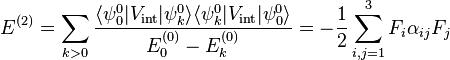
With the components of the polarizability tensor α defined by

  

The energy E(2) gives the quadratic Stark effect.

Because of their spherical symmetry the polarizability tensor of atoms is isotropic,

 

This is the quadratic Stark shift for atoms. For many molecules this expression is not too bad an approximation, because molecular tensors are often reasonably isotropic.

Quantum-confined Stark effect

In a semiconductor heterostructure, where a small band gap material is sandwiched between two layers of a larger band gap material, the Stark effect can be dramatically enhanced by bound excitons. This is because the electron and hole which form the exciton are pulled in opposite directions by the applied electric field, but they remain confined in the smaller band gap material, so the exciton is not merely pulled apart by the field. The quantum-confined Stark effect is widely used for semiconductor-based optical modulators, particularly for optical fiber communications.