Soil Mechanics 3(2+1)

LESSON 22. One Dimensional Consolidation

Figure 22.1 shows a clay layer in between two sand layers (drainage layers). Clay layer is subjected a uniformly distributed stress σ. A small soil element of dimension dx, dy and dz is chosen at a depth of ‘z’ from the top of the clay layer or consolidating layer. The continuity equation of the element can be written as:

\[\left( {{{\partial {v_x}} \over {\partial x}} + {{\partial {v_y}} \over {\partial y}} + {{\partial {v_z}} \over {\partial z}}} \right)dx\,dy\,dz={{\partial V} \over {\partial t}}\]                (22.1)

where v_x, v_y and v_z are the velocity in x, y and z direction, respectively. δV is the change in volume. For 1-D consolidation, Eq. (22.1) can be written as:

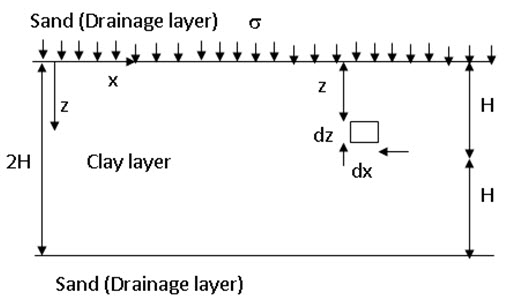
 Fig. 22.1. 1-D consolidation.

\[\left( {{{\partial {v_z}} \over {\partial z}}} \right)dx\,dy\,dz={{\partial V} \over {\partial t}}\]                    (22.2)

Now according to Dercy’s law,

\[{v_z}={k_z}{{\partial h} \over {\partial z}}\]                        (22.3)

where k_z is the coefficient of permeability, h is the head which causes flow during consolidation.  The Eq. (22.3) can be written as:

\[{{\partial {v_z}} \over {\partial z}}={k_z}{{{\partial ^2}h} \over {\partial {z^2}}}\]                          (22.4)

The head h can be expressed as:

\[h={u \over {{\gamma _w}}}\]                                (22.5)

where ‘u’ is the excess pore water pressure and \[\gamma\]_w is the unit weight of water. Combining Eq. (22.2) and Eq. (22.4), one can write

\[{{{k_z}} \over {{\gamma _w}}}{{{\partial ^2}u} \over {\partial {z^2}}}dx\,dy\,dz={{\partial V} \over {\partial t}}\]                           (22.6)

Now rate of change of volume can be written as:

\[{{\partial V} \over {\partial t}}={\partial\over {\partial t}}\left( {dx\,dy\,dz} \right)\]                     (22.7)

If volume of soil element V = dx dy dz and e₀ is the initial void ratio, then the volume of voids (V_v) can be written as:

\[{V_v}={{{e_0}}\over {1 + {e_0}}}dx\,dy\,dz\]                    (22.8)

When V_v is to experience change, e will be a variable. Thus, Eq. (22.8) can be written as:

\[{V_v}={e \over {1 + {e_0}}}dx\,dy\,dz\]                           (22.9)

The change in volume is due to the change in volume of voids. Thus, combining Eq. (22.7) and Eq. (22.9) one can write

\[{{\partial V}\over{\partial t}}={\partial\over{\partial t}}\left({{e\over{1 + {e_0}}}dx\,dy\,dz}\right)\]                                     (22.10)

Now, volume of solid soil (V_s) grains is a constant and can be expressed as:

\[{V_s}={1 \over {1 + {e_0}}}dx\,dy\,dz\]                            (22.11)

Thus, Eq. (22.10) can be written as:

\[{{\partial V}\over{\partial t}}={\partial\over{\partial t}}\left({{e\over{1 + {e_0}}}dx\,dy\,dz}\right)={{dx\,dy\,dz}\over{1 + {e_0}}}{{\partial e}\over {\partial t}}\]                              (22.12)

A time t =0, applied stress is equal to excess pore water pressure. Thus, du = -dσ , the negative sign means as the excess pore water pressure decreases effective stress increases. Again, de = -a_v \[d\bar \sigma\] . Thus, de = a_v  du. Eq. (22.12) can be written as:

\[{{\partial V}\over{\partial t}}={{dx\,dy\,dz}\over{1+{e_0}}}{{\partial e}\over{\partial t}}={{dz\,dy\,dz}\over{1 + {e_0}}}{a_v}{{\partial u}\over {\partial t}}\]                          (22.13)

Combining Eq. 22.6) and Eq. (22.13), one can get

\[{{{k_z}}\over{{\gamma _w}}}{{{\partial ^2}u}\over{\partial{z^2}}}dx\,dy\,dz={{dz\,dy\,dz}\over {1 + {e_0}}}{a_v}{{\partial u}\over{\partial t}}\]                                         (22.14)

Thus,

\[{{\partial u}\over{\partial t}}={{{k_z}}\over {{\gamma _w}}}{{1 + {e_0}}\over {{a_v}}}{{{\partial ^2}u}\over{\partial {z^2}}}\]                      (22.15)

\[{{\partial u} \over {\partial t}}={c_v}{{{\partial ^2}u} \over {\partial {z^2}}}\]                      (22.16)

where c_v is the coefficient of consolidation and can be expressed as:

\[{c_v}={{{k_z}}\over{{\gamma _w}}}{{1 + {e_0}}\over {{a_v}}}={{{k_z}}\over{{\gamma _w}{m_v}}}\]                             (22.17)

where m_v is the compressibility of soil and can be expressed as:

\[{m_v}={{{a_v}} \over {1 + {e_0}}}\]                          (22.18)

The boundary and initial conditions are:

• At t = 0, u = u_i and u_i = σ

• At t → , u = 0 for all z

• t >0, z = 0, u = 0

• t >0, z = 2H, u = 0 (if drainage layer is present in top and bottom of the consolidating layer).

In Terzaghi’s solution, three non-dimensional factors are presented as:

Drainage depth ratio, \[Z={z \over H}\]                        (22.19)

Tine factor, \[{T_v}={{{c_v}t} \over {{H^2}}}\] (if drainage layer is present in top and bottom of the consolidating layer)            (22.20)

Time factor, \[{T_v}={{{c_v}t} \over {{{\left( {2H} \right)}^2}}}\]                    (22.21)

Thus, \[t \propto {{{H^2}} \over {{c_v}}}\]                        (22.22)

Degree of consolidation, \[{U_z}={{{u_i} - {u_z}} \over {{u_i}}}=1-{{{u_z}} \over {{u_i}}}\]                          (22.23)

In Terzaghi’s solution, U_z is expressed in terms of Fourier series as:

\[{U_z}=1-\sum\limits_{n = 0}^ \propto{{f_1}(Z){f_2}({T_v})}\]                               (22.24)

• At t = 0, T_v = 0  and U_z = 0 for all values of Z

• At t → , T_v → µ  and U_z = 1 or 100% for all values of Z

Thus, degree of consolidation is a function of T_v. For example, U = 50% if T_v = 0.197 and U = 90% if T_v = 0.848. Keeping soil parameters constant, as the time increases degree of consolidation also increases. 

 

References

Ranjan, G. and Rao, A.S.R. (2000). Basic and Applied Soil Mechanics. New Age International Publisher, New Delhi, India.

Suggested Readings

Ranjan, G. and Rao, A.S.R. (2000) Basic and Applied Soil Mechanics. New Age International Publisher, New Delhi, India.

Arora, K.R. (2003) Soil Mechanics and Foundation Engineering. Standard Publishers Distributors, New Delhi, India.

Murthy V.N.S (1996) A Text Book of Soil Mechanics and Foundation Engineering, UBS Publishers’ Distributors Ltd. New Delhi, India.