Site pages
Current course
Participants
General
MODULE 1. Fundamentals of Soil Mechanics
MODULE 2. Stress and Strength
MODULE 3. Compaction, Seepage and Consolidation of...
MODULE 4. Earth pressure, Slope Stability and Soil...
Keywords
LESSON 28. Slope Stability
28.1 Introduction
Slopes can be natural (in hillside and valley, coastal or river cliffs) or man-made (embankments for highways and railways, earth dams, excavation). In case of slopes existing forces cause the soil movements from higher point to lower point and slopes become more stable. If soil mass moves in a slope it is referred as slope failure. The slope failure may occur due to earthquake also. Slopes can be infinite slopes (as shown in Figure 28.1a) and finite slopes (as shown in Figure 28.1b).

Fig. 28.1. (a) Infinite slope and (b) finite slope.
28.1.1. Infinite Slope
In case infinite slopes failure takes place due to the sliding of soil mass along a plane parallel to the slope at a certain depth and this type of failure is referred as translational slides. Figure 28.2 shows the forces acting on an element in the infinite slope. The soil is assumed to be homogeneous. In the Figure 28.2, W is the weight of the element. From the figure it is written as:
\[W=\gamma \,zb\cos \beta\] (28.1)
\[{\sigma _n}={{W\cos \beta } \over b}=\gamma \,z{\cos ^2}\beta\] (28.2)
\[\tau={{W\sin \beta } \over b}=\gamma \,z\cos \beta \sin \beta\] (29.3)
where σn is the normal stress, t is the shear stress and \[\gamma\] is the unit weight of the soil.

Fig. 28.2. Forces acting on an element in the infinite slope.
Cohesionless Soil
For cohesionless soil, the shear strength can be written as:
\[{\tau _f}={\sigma _n}\tan \phi '=\gamma \,z{\cos ^2}\beta \tan \phi '\] (28.4)
where tf is the failure shear strength and ø' is the angle of shearing resistance or angle of internal friction.
Thus, factor safety (F) can be written as:
\[F={{Shear\;Strength} \over {Shear\;Stress}}={{\gamma \,z{{\cos }^2}\beta \tan \phi } \over {\gamma \,z\cos \beta \sin \beta }}={{\tan \phi '} \over {\tan \beta }}\] (28.5)
Figure 28.3 shows the effective forces acting on an element in the infinite slope. The position of water table is also shown in the figure. The effective normal stress can be written as:
\[{\sigma '_n}={{(W-{\gamma _w}hb\cos\beta )\cos\beta}\over b}=(\gamma\,z\cos\beta-{\gamma _w}h\cos\beta)\cos\beta\]
\[=(\gamma \,z - {\gamma _w}h){\cos ^2}\beta\] (28.6)
\[\tau={{W\sin \beta } \over b}=\gamma \,z\cos \beta \sin \beta\] (28.7)
where Yw is the unit weight of water.
\[F={{Shear\;Strength}\over{Shear\;Stress}}={{{{\sigma '}_n}\tan \phi}\over\tau }={{(\gamma \,z - {\gamma _w}h){{\cos }^2}\beta\tan\phi}\over{\gamma \,z\cos \beta \sin \beta }}=\left({1 - {{{\gamma _w}h}\over {\gamma \,z}}} \right){{\tan\phi '}\over{\tan\beta}}\] (28.8)
If water table is at the top i.e z=h then,
\[F=\left({1 - {{{\gamma _w}} \over \gamma }} \right){{\tan \phi '}\over{\tan \beta }}\] (28.9)
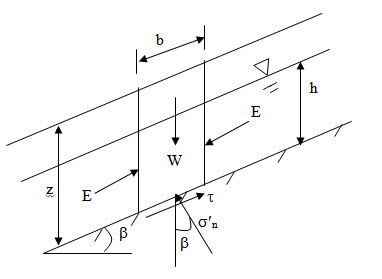
Fig. 28.3. . Effective forces acting on an element in the infinite slope.
Cohesive Soil
In case of c-ø soil, the shear strength can be written as:
\[{\tau _f}=c' + {\sigma _n}\tan \phi '=c' + \gamma \,z{\cos ^2}\beta \tan \phi '\] (28.10)
\[F=={{c' + \gamma \,z{{\cos }^2}\beta \tan \phi '} \over {\gamma z\cos \beta \sin \beta }}\] (28.11)
For F = 1, the depth z is called as critical depth (hc). Thus, putting F=1 and z=hc in Eq. (28.11), one can get
\[{h_c}={{c'} \over {\gamma (\tan \beta-\tan \phi '){{\cos }^2}\beta }}\] (28.12)
For seepage parallel to the slope,
\[F={{c' + (\gamma z - {\gamma _w}h){{\cos }^2}\beta \tan \phi'}\over{\gamma z\cos\beta\sin\beta }}\] (28.13)
\[{h_c} = \frac{{c'}}{{\gamma (\tan\beta-\frac{{{\gamma _w}}}{\gamma}\tan\varphi '){{\cos}^2}\beta}}\] (28.14)
The stability number (Sn) can be written as:
\[{S_n}={{c'} \over {\gamma {h_c}}}=(\tan \beta-\tan \phi '){\cos ^2}\beta\] (28.15)
References
- Ranjan, G. and Rao, A.S.R. (2000). Basic and Applied Soil Mechanics. New Age International Publisher, New Delhi, India.
Suggested Readings
-
Ranjan, G. and Rao, A.S.R. (2000) Basic and Applied Soil Mechanics. New Age International Publisher, New Delhi, India.
-
Arora, K.R. (2003) Soil Mechanics and Foundation Engineering. Standard Publishers Distributors, New Delhi, India.
-
Murthy V.N.S (1996) A Text Book of Soil Mechanics and Foundation Engineering, UBS Publishers’ Distributors Ltd. New Delhi, India.