LESSON 17.

17.1 METHOD OF SECTIONS

For a member near to supports can be analysed with the help of method of joints and for members remote from supports can be quickly analysed with the help of method of sections.

  • In this method a section line is passed through the members, in which forces are to be determined in such a way that not more than three members are cut.
  • Then any of the cut part is then considered for equilibrium under the action of internal forces developed in the cut members and external forces on the cut part of the truss.
  • The condition of equilibrium, i.e \[\sum V = 0,\sum H = 0,\sum M=0\]  are applied to the cut part of the truss under consideration. As three equations are available, therefore, three unknown forces in the three members can be determined.
  • If the magnitude of a force comes out to be positive then the assumed direction is correct. If the magnitude of a force is negative then reverse the direction of that force.

Example: Find the forces in the members PR and PQ of the truss loaded as shown in Fig.17.1, using method of sections.

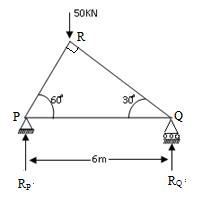
Module 5 Lesson 17 Fig.17.1

Fig.17.1

 Solution: PR = 6 cos60° = 3 m

QR = 6 sin60° = 6 . \[{{\sqrt 3 } \over 2}\] = 3 \[\sqrt 3\]  = 5.19 m

Determination of reactions.

Let RP and RQ be the reactions at P and Q.

Taking moments about P,

RQ × 6 = 50 × PR. cos60°

6 RQ = 50 × 3 × \[{1 \over 2}\]
RQ = 12.5 kN

RP + RQ = 50

RP = 50 – 12.5 = 37.5 kN

Passing a section 1-1, thereby cutting the truss in two parts.

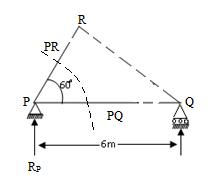
Module 5 Lesson 17 Fig.17.2

Fig.17.2

Considering equilibrium of the left part. The part part of the truss is shown in Fig.17.2. This part is in equilibrium under the action of one external force RP = 37.5 kN and other two internal unknown forces PR and PQ in the members PR and PQ respectively. The directions of PR and PQ both are considered as tensile as marked in Fig.17.2

Determination of force PR

Taking moment of all forces about Q.

The moment of force PQ about point Q is zero.

Therefore, RP × 6 + (PR × QR) = 0 ( because QR is perpendicular distance between force PR and point Q i.e 5.19 m)

(37.5 × 6) + PR × 6.sin 60°  = 0

PR = -   \[{{225} \over {6\sin 60^\circ }}\]  = -   \[{{37.5} \over {0.866}}\] = - 43.30 kN

-ve sign indicates that the assumed direction is wrong. This force is actually compression force.

Hence, PR = 43.30 kN

Determination of force PQ

If we take the moments of all forces about point R, then PR will be eliminated and there will be only one unknown force PQ.

Hence, taking moment about point R,

-(PQ × PR.sin60° ) + (RP × PR.sin60° ) = 0                                                             (\[\sum M = 0)\]

-(PQ × 3 × 0.866) + (37.5 × 3 × 0.5) = 0

2.598 PQ = 56.25

PQ = + 21.65 kN

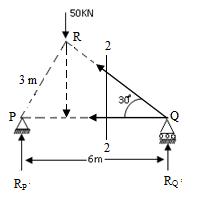
 Module 5 Lesson 17 Fig.17.3

Fig.17.3

The positive sign indicates that the assumed direction is correct. This force is tensile force.

Now if the in member QR is also to be determined then we will have to take another section 2-2 so as to cut the member QR and PQ, as shown in Fig.17.3 Now considering equilibrium of right part of truss, under the section of two internal forces QR , PQ and one external force RQ = 12.5 kN, we can apply condition (\[\sum M = 0)\]  , if we take moment about P, then forces PQ will be eliminated and only one unknown force QR will remain. Hence by taking moment about P, we get (QR × 3) + (12.5 × 6) = 0

QR = - \[{{75} \over 3}\]  = -25 kN

Negative sign indicates the assumed direction is wrong. This force is actually compressive. Similarly if we take moment about R, force QR is eliminated and PQ = 21.65 kN (tensile).

Example: Determine the forces in the members DE, BE and AB of the truss, shown in Fig.17.4.

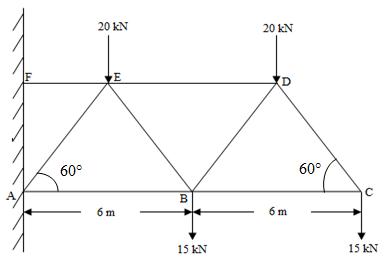
Module 5 Lesson 17 Fig.17.4

Fig.17.4

Solution: Pass a section X-X in such a way so that three desired members DE, BE and AB are cut. Now consider the right part of the cut truss as shown in Fig.17.5.Let F1, F2 and F3 be the forces in the members DE, BE and AB respectively.

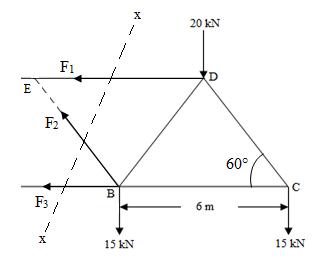
Module 5 Lesson 17 Fig.17.5

Fig.17.5

Determination of F1,

Taking moments about B, so that moments of the forces F2 and F3 are eliminated

We have, - F1 × 6 sin60° + (20×3) + (15×6) = 0

-5.196 F1 + 60 + 90 = 0

F1 = 28.868 kN (Tensile)

Determination of F3,

Taking moments about E

F3 × 6 sin60° + (15×3) + (20×6) + (15×9) = 0

5.196 F3 + 45 + 120 + 135 = 0

F3 = 57.737 kN (Compressive)

Determination of F2,

Applying equilibrium condition

F2 sin60° = 20 + 15 + 15 = 50

F2 = 57.735 kN (Tensile)

Last modified: Tuesday, 10 September 2013, 9:05 AM