Module 1. Conduction heat transfer

Lesson 3

PROBLEMS ON HEAT CONDUCTION THROUGH PLANE/COMPOSITE WALLS HAVING VARIABLE THERMAL CONDUCTIVITY

Q. 1: Determine the hourly loss of heat through a brick wall 5 m long, 3 m high and 250 mm thick. If wall surface temperature. t₁=20°C and t₂ = -30°C. The λ_brick = 0.6 kcal/m-hr-°C.

Solution:

Conductivity, λ = 0.6 kcal/m-hr-°C.

Thickness, δ = 250 mm = 250 × 10^-3 m = 0.25 m

q = 120 [kcal/m²-hr]

q = loss of heat through 15 m² area of brick = q x A = 120 x 15 = 1800 kcal/hr

Q = 1800 kcal/hr.

Q. 2: Determine 𝛌, thermal conductivity of a wall if q = 100 kcal/m²-hr at thickness, 𝛅 = 30 mm and ∆t = 30°C.

Solution:

Heat transferred, q = 100 kcal/m²-hr

Thickness, 𝛅 =30 mm = 30 x 10^-3m = 0.03 m

∆t = 30°C

𝛌 = 0.1 [kcal/m-hr-^oC]

Q. 3: Determine the rate of heat flow through a flat fire clay wall 𝛅 = 0.5 m & also find true distribution of temperature. If t₁ = 1000°C & t₂ = 0°C, 𝛌 =1.0 x (1+0.001t).

Solution:

q = rate of heat flow, λ_m= mean conductivity, t_m = mean temperature.

λ_m = 1.0[1+0.001×500) = 1.5 [kcal/m-hr-^oC]

For true distribution of temperature:

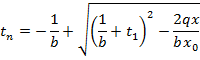
b = 0.001, t₁= 1000, x₀ = 1.

Equations of the temperature curve at any location =

So, for different values of x; x = 0, 0.1, 0.2, 0.3, 0.4, 0.5

True distribution of temperature

Equation of temperature curve

0.1

0.2

0.3

0.4

0.5

1000

844

673.3

488.2

264.9

1000

800

600

400

200

Q. 4: Determine the quantity of heat passing per hour through 1 m² area of a boiler wall, if it is 20 mm thick and the thermal conductivity of its material is 50 kcal/m-hr-°C. The inner surface of the wall is covered by a layer of scale of thickness 2 mm whose thermal conductivity is 1.0 kcal/m-hr-°C. The temperature of the outer surface is 250°C and of the inner surface is 200°C.

Solution:

Thermal resistance =

δ = Thickness

λ = Thermal conductivity

Thermal resistance of outer surface =

δ₁, (Thickness)= 20 mm = 0.02 m

λ₁, Thermal conductivity of outer Surface = 50 kcal/m-hr-°C

Thermal resistance of outer surface = 0.02/50 = 4x 10^-4 [m²-hr-°C/kcal]

Thermal resistance of inner surface =

δ₂,Thickness = 2 mm = 0.002 m

λ₂,Thermal conductivity of inner surface = 1.0 kcal/m-hr-°C

Thermal resistance of inner surface = = 0.002/1 = 20x 10^-4 [m²-hr-°C/kcal]

Quantity of heat passing,

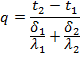
t₁ = temperature of outer surface, t₂ = temperature of inner surface

t₂ = 250°C, t₁ = 200°C

= 2.08 x 10⁴ [kcal/m²-hr] = 20800 [kcal/m²-hr]

t = t₁ – q = Temperature of contact = 250-20,800 x 4x10^-4

t = 241.7°C

Q. 5: The rate of heat flow (q) through a plane wall of thickness δ = 50 mm is70 watt/m². Determine the difference between the temperatures of wall surfaces and the numerical values of the temperature gradient through the wall if it is made from

(a) Brass whose λ = 70 watt/m-°C

(b) If wall is made of red brick whose λ = 0.7 watt/m-°C

Solution:

Temperature gradient = ∆t/δ

q = Rate of heat flow

λ = Thermal conductivity

δ = Thickness

∆t = Difference between temperature of wall surfaces.

(a) Brass

q = 70 watt/m²

δ = 50 mm = 50 x 10^-3 = .05 m

λ = for brass = 70 watt/m-°C

Temperature Gradient = 0.05/0.05 = 1°C/m

(b) For Red Brick

λ for red brick = 0.7 watt/m-^°C

5°C = ∆t

Temperature Gradient = 5/0.05 = 100°C/m

λ for cork = 0.07 watt/m-°C

∆t = 50C

Temperature Gradient = ∆t /δ = 50/0.05 = 1000°C/m

Q. 6: Determine the loss of heat Q (watts) through a wall laid of lead brick of length 5 m, height 4 m and thickness 0.25 m, if the temperature of the surfaces of the wall are maintained at 110°C & 40°C. Assume λ_brick = 0.7 watt/m-°C.

Solution:

λ, thermal conductivity = 0.7 watt/m-°C

δ = thickness = 0.25 m

∆t, temperature difference of surfaces = (110-40) = 70°C

= 196 watt/m²

Q, loss of heat through 20 m² area of wall = q x A= 196 x 20 = 3920 watt

Q = 3920 watt

Q. 7: It is necessary to insulate a flat surface such that the loss of heat from unit area of this surface per unit time will not exceed 450 watt/m². The temperature of the surface underneath the layer of insulation is the 450°C and the layer temperature of the external surface of the insulating layer is 50°C. Determine the thickness of insulation for the following two cases

(a) The insulation is made from sobelite for which, λ = [0.09 + 0.0000874 t] watt/m°C.

(b) The insulation is made from Asbestos cement for which λ = [0.09 + 0.000146 t] watt/m°C.

Solution, Case a:

λ = [0.09 + 0.0000874 t] watt/m-°C

t = 50°C

λ₁ = [0.09 + 0.0000874 x 50] = 0.09437 watt/m-°C.

t = 450°C

λ₂ = [0.09+0.0000874×450] = 0.12933 watt/m-^oC