Module 1. Conduction heat transfer
Lesson 4
CONDUCTION THROUGH A CYLINDRICAL WALL (HOMOGENOUS, COMPOSITE) TEMPERATURE CURVE IN A CYLINDRICAL WALL
4.1 Conduction through a Homogeneous Cylindrical Wall (Tube/Pipe)
Let us consider a cylindrical wall of l m long with inner radius r1 and outer radius r2. Let us assume λ of the material is constant. The inner and outer faces are held at constant temperatures t1 and t2 under the condition that t1>t2. Therefore temperature varies only radially and we can assume that this radial direction is x-direction. Thus temperature field is one dimensional and the isothermal surfaces are cylindrical surfaces possessing a common axis with the tube. (Fig. 4.1 (a))
Let us consider an annular layer of
radius r and thickness dr inside the wall limited by two cylindrical
isothermal surfaces. Let us apply Fourierís law:
††††††††††† ![]()
††††††††††††††† ![]()
![]()
††††††††††††††† ![]()
Let us subject this solution to boundary
conditions [r = r1, t = t1] and [r = r2, t = t2]
††††††††††† ![]()
††††††††††††††† ![]()
††††††††††††††† ![]()
![]()
††††††††††††††† ![]()
Hence the amount of heat flowing through the wall of the tube per hour is directly proportional to λ, l (length of the tube) and the ∆t (temperature difference = t1-t2) and inversely proportional to the natural logarithm of the ratio of outer radius to inner radius and the radii ratio can be replaced by that of diameters. This equation is the calculation formula for conduction through a homogeneous cylindrical wall. It remains true for the case if t1<t2. In that case, the flow of heat is directed from the outer surface to the inner.
By inserting the value of the constant C
![]()
††††††††††††††† ![]()
By readjustment, and inserting the value of Q
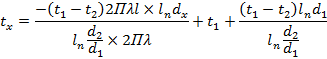
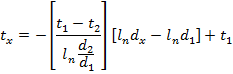
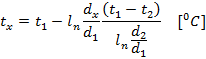
This temperature distribution curve is a logarithmic curve which means that the temperature inside a homogeneous cylindrical wall varies along a logarithmic curve provided thermal conductivity is constant.
If λ is not constant:
If we take into consideration, the dependence of λ on temperature assuming that
λ = λ0 (1 + bt)
Then the equation of temperature
distribution curve into cylindrical wall will acquire the form
![]()
The amount of heat passing through the wall of the tube per hour is applicable either to 1 m of length or a unit of inner or outer surface area.
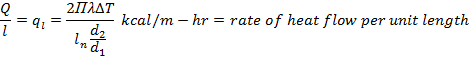
††††††††††††††† ![]()
![]()
4.2 Composite Cylindrical Wall
Let us consider a composite cylindrical wall of three heterogeneous layers. The adjacent surfaces are of the same temperature due to the assumption that there is perfect contact between them. The diameter and thermal conductivities of individual layers are known.
The temperatures t1 and t4 of the inner and outer surfaces of the composite wall are also known. The contact temperatures t2 and t3 are unknown. (Fig. 4.1 (b))
Under steady state conditions, the amount of heat passing through each layer is the same and constant. Therefore we can write the following equations, i.e.
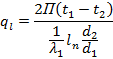
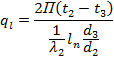

Rewriting, we get
![]()
![]()
![]()
Adding vertically
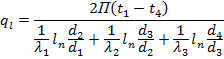
By analogy, for a composite wall of Ďní layers
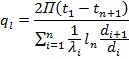
By inserting the value of x we can obtain the unknown temperatures
![]()
![]()