Module 1. Conduction heat transfer

Lesson 5

PROBLEMS ON CONDUCTION THROUGH HOMOGENOUS/COMPOSITE WALL, HAVING VARIABLE THERMAL CONDUCTIVITY, CONDUCTION THROUGH A HOLLOW SPHERE

5.1  Problems

Q. 1: The brick work of a terrace is built up of layers laid of fire clay and red brick and the space between the two layers of brick work is filled with crushed diatomite brick. The fire clay is 120 mm thick. The thickness of the diatomite filling is 50 mm and thickness of the red brick layer is 250 mm. The thermal conduction of these three materials are 0.93, 0.13, 0.7 W/m°C. What should be the thickness of red brick layer of the brick work which is to be laid without the diatomite filling between the two layers so that the heat flux through the brick work remain constant.

Solution:

Heat conduction with diatomite filling

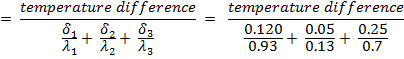
 Heat flux without diatomite filling

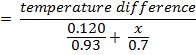
q₁ = q₂

0.385 + 0.357 =

x  = 0.5194 m

or  x = 519.4 mm

Q. 2: The wall of a steam boiler furnace which is not fitted with waterfalls is made up of a layer of foamed fire clay of thickness 125 mm and a layer of red brick 500 mm thick. The two layers fit each other tightly. The wall temperature inside boiler furnace is 1100°C and outside is 50°C. The thermal conductivity of foamed fire clay is (0.28 + 0.00025 t) and that of red brick is 0.7W/m°C. Calculate the amount of heat lost from 1 m² of the furnace wall by conductance. Also find the temperature of in furnace layer.

Solution:

= 575°C

= 0.412 W/m°C

Amount of heat lost q

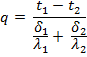
q =  1032.45 kj/m²

t₂ = 1100 – 11032.45 x 0.303

t₂ = 787.17°C

Q. 3: The thickness of the layer of red brick in the wall of boiler furnace setting, considered in previous problem, is to be reduced by 2 times. The space between the two layers of the setting is filled with crushed diatomite whose thermal conductivity λ = 0.113 + 0.0002 W/m°C. What should be the thickness of diatomite filling to ensure the same loss of heat with inside and outside wall temperature remaining same as in previous problem.

Solution:

= 0.245 W/m°C

q is same

∴ q 1^st case = q 2^nd case

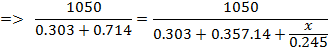
x = 0.874 m or x = 87.4 mm

Q. 4: A steam pipe line of diameter d₁/d₂ = 100/110 mm with λ₁ = 50 W/m°C is covered with two layer of insulation of equal thickness i.e. 50 mm. Temperature of inner surface is t₁ = 250°C and temperature of outside surface is t₄ = 50°C. Determine loss of heat through insulation from length of 1 m of pipeline and interface temperature.

Solution:

            λ₂ = 0.06 W/m°C                                             λ₃ = 0.12 W/m°C

            d₁ = 100 mm                                                   d₂ = 110 mm

            d₃ = 210 mm                                                   d₄ = 310 mm

t₂   = 249.9°C

If the layers are interchanged:

Q. 5: A steam pipe line with 160/170 mm in diameter covered with layer of insulation of δ = 100 mm with thermal conductivity depending on temperature in following way -  λ_ins = 0.062 (1+0.36 × 10^-2t) W/m°C. Determine amount of heat loss from length of 1 m of pipeline and temperature of its inner surface if temperature of outer is 300°C. Temperature of outer surface of insulation should not exceed 50°C. λ for pipe line is 50 W/m°C.

Solution:

= 175°C

q₁ = 204.59 kcal/m-hr

λ_inst = 0.062 {1 + 3.63 x 10^-2(1.75)}

= 0.062 (1.635)

= 0.10137 W/°C

Q. 6: A steam pipe line of 170/160 mm in diameter covered with layer of insulation thickness of 1^st layer is 30 mm and that of 2^nd is 50 mm. Thermal conductivity of pipe insulating are 50, 8.15 and 0.008 respectively. Inner temperature is 300°C outer temperature is 50°C. Determine quantity of heat lost per unit length and also find layer contact temperature.

Solution:

         δ₁ = 30 mm                                          δ₂ = 50 mm

         d₂ = 170 x 10^-3                                                d₁ = 160 x 10^-3

         d₃ = d₂ + 60 mm                                  d₄ = d₃ + 100 mm

              = 230 x 10^-3                                         = 330 x 10^-3 m

         λ₁ = 50 kcal/m-hr-°C

         λ₂ = 0.15 kcal/m-hr-°C

         λ₃ = 0.008 kcal/m-hr-°C

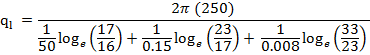
= 240 kcal/m-hr

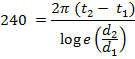
Then   

= 222.8

Q. 7: A steam pipe line of 150/160 mm in diameter is covered with layer of heat insulating material of thickness 100 mm. Thermal conductivity of tube is 50 W/m°C or kcal/m-hr-°C and λ_ins,mat = 0.09 kcal/m-hr-°C. Temperature of pipeline inside surface is 400°C and temperature of the outside surface of insulating surface is 50°C. Find loss of heat from length of 1m of pipeline and temperature at interface of insulation.

Solution:

            d₁ = 150 x 10^-3            m                                 d₂ = 160 x 10^-3 m

            d₃ = 360 x 10^-3 m

Q. 8: A reinforced concrete smoke stack with an inner diameter d₂ = 800 mm, outer diameter d₃ = 1300 mm must be lined with a refractory on the inside. Determine the thickness of the refractory lining and the temperature of outer surface of the smoke stake (t_w3) under the conditions that the loss of heat from length of 1 m of the smoke stack must not exceed 2000 W/m and the temperature of the inner surface of the reinforced concrete smoke stack (t_wr) should not exceed 200°C. The temperature of the inner surface of lining is t_w1 = 425°C. The thermal conductivity of the lining material λ₁ = 0.5W/m°C and of concrete λ₂ = 1.1W/m°C.

Solution:

For lining,

d₂ = 800 mm

Q = 2000 W/m

t₁ = 425°C       t₂ = 200°C

λ₁ = 0.5 W/m°C

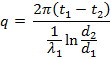
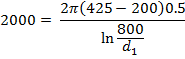
Thickness of lining = δ =
t₂ = 200°C

d₂ = 800 mm

d₃ = 1300 mm

q = 2000 W/m

λ₂ = 1.1 W/m°C

t₃ = temperature of outer surface of smoke stack.

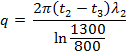
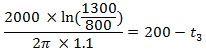
5.2  Conduction through a Hollow Sphere

Let us consider the flow of heat through wall of hollow sphere with inner radius r₁ and outer radius r₂^.  The sphere is made up of homogeneous material of constant thermal conductivity (λ).

The inner and outer surfaces are kept at constant temperatures t₁ and t₂. Let us assume that t₁ > t₂.

Temperature varies only in the direction of radius. The wall is limited by concentric spherical isothermal surfaces. Let us take a thin layer between two spherical surfaces with a radius r and let us assume that thickness of surface is infinitesimally small = dr.

The surface of this layer is thermal. Now let us apply Fourier’s law. The amount of heat flowing through that layer per hour Q = -λF

                                                             = - λ (4πr²) kcal/hr.

(Fig 5.1: Homogeneous spherical wall)

This is the governing differential equation.

On separating the variables and integrating, we can have the solution.

Subjecting this general solution to the boundary conditions.

r = r₁,               t = t₁                            and                              r = r₂                t = t₂

We get the particular solutions,

On subtracting

From this solution, we can determine Q

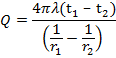
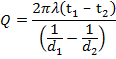
Where δ = thickness of wall =

These equations can be used to calculate heat conduction through a hollow spherical wall. Inserting the value of C and the value of Q, we can obtain the temperature distribution curve.

t_x = temperature at any location in a spherical wall.

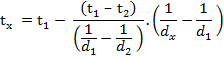
This equation of temperature curve is that of hyperbola. Therefore, the distribution of temperature in a spherical wall is represented by a hyperbola.