Module 2. Convection heat transfer

Lesson 10

DERIVATION OF EQUATION OF FLOW

10.1  Equation of Flow

The equation of heat conduction in moving fluids includes, in addition to temperature, the three variables w_x, w_y and w_z. This means that in a moving fluid the temperature field depends on the distribution of velocity. The latter is described by the differential equation of flow derived on the basis of the second Newton law: force equals mass by acceleration.

Consider in the flow of fluid an elementary parallelepiped with sides dx, dy and dz. Three forces act on the particle: inertia force, pressure force and friction force. Let us find the projection of these forces upon the x-axis.

a) The inertia force is applied at the centre of gravity of the element d𝜐. The component of the force along the x-axis is equal to the product of the component of acceleration due to gravity g_x[m/sec²] by the mass of the element m = ϱ d𝜐

 g_x ϱ d𝜐 = g_x ϱ dx dy dz                                                                     ......... (a)

b) The pressure force is determined on the basis of the following consideration. If the specific pressure of fluid exerted upon the upper face of the element is p [kg/m²], then a force p dy dz acts upon the area dy dz. The lower face of the element is subjected to a specific pressure and a force acts on this face. Here, the minus sign indicates that this force acts in a direction opposite to that of fluid flow. The resultant force is equal to the algebraic sum of two applied forces.

......... (b)

c) The flow of fluid is always accompanied by the appearance of a friction force. The equation of the friction force may be derived by considering the flat laminar flow, in which the velocity components w_x changes only in the direction of y-axis. In this event the friction force appears only on the side faces of the element considered. The velocity of particles at the left face of the element is less than that of the particles within the element; therefore, in the cross-section y the friction force is directed against the flow of fluid and is equal to ( ̶  s dx dz). The opposite is true of the right face of the element. Here, the particles move at a velocity exceeding that of the particles within the element: therefore, in the cross-section y + dy the friction force acts in the direction of flow and is equal to

The resultant of these forces is equal to their algebraic sum

......... (c)

Here s is the friction force per unit area,  according to Newton’s law. Substituting this expression of s into equation (c), we get

......... (d)

This comparatively simple expression, however, applies only to one-dimentional flow, while generally, when w_x varies along the three directions, the components of the friction force along the x-axis is determined by the following expression

......... (e)

Adding up expression (a), (b) and (e), we get the x-axis components of the resultant of all the forces acting upon the considered elementary particle of volume dv

......... (f)

According to the second law of machines, this resultant force is the product of the mass of the element ϱ dυ by its acceleration

......... (g)

Equating (f) and (g) and cancelling dυ, we finally get:

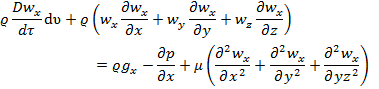......... (h)

 All the terms of this equation have the units of force referred to unit volume, kg/m³.

The components of the resultant force along the y-and and z-axes can be obtained in a similar way, namely,

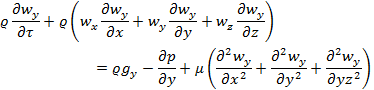......... (h^ʼ)

......... (h^ʼʼ)

This system of three equations (h, hʹ, hʹʹ) is known as the Navier-Stoke’s differential equation for incompressible viscous liquids. The equation applies both to laminar and turbulent flow.