Module 3. Dimensional analysis and heat transfer

Lesson 12

CONDITIONS OF HYDROMECHANICAL SIMILARITY: DIMENSIONLESS NUMBERS

12.1  Conditions of Hydro-mechanical Similarity

Hydro-mechanical similarity determines the conditions in which similar flows occur in geometrically similar systems. Let us examine these conditions for the incompressible fluid flow.

Equation of continuity

Equation of flow

And for the second system, respectively

As the considered processes are similar, from the definition of similarity we have

These relationships are used to express all the variables of the second system by the variables of the first system in the following manner:

Substituting the values in equation of second system

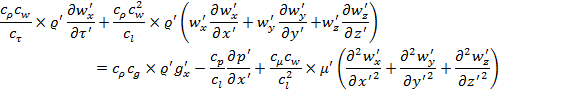
Both systems are now expressed by the variables of the first system. These variables from both systems must be determined in a similar manner. The latter stipulation is possible only if the equations are identical, and they require the dimensionless groups made up of the similarity constant to be cancelled from the system.

From the continuity equation it follows that

This relationship does not limit the choice of similarity constant. Because the equation remain identical for any values of the ratio .

From the equation of flow

Investigating the members in pairs, we have

Such re-arrangement gives

Where

Ho = the homochronocity number

            Fr = the Froude number

            Eu = the Euler number

            Re = the Reynolds number

The hydro-mechanical similarity of two or several systems, therefore, requires the numerical values of the Ho, Fr, Eu and Re numbers to be equal at any corresponding points of the systems.

In practical consideration these dimensionless numbers are modified with a view to give them a more convenient form easy to understand and interpret. So we have,

Where G_a = Gallilian number

Where Ar = Archimedes Number

ρ, ρ₀= fluid density at two different point of system.

If difference in density depend upon temperature difference then,

β = Fluid Expansion Factor

Substituting these values, we get

Where Gr = Grashoff Number

It should be clearly understood that all these dimensionless terms Fr, Ga, Ar, Gr are identical because these numbers are four different forms of one and same criteria.

Similarly Euler Number is also modified. The pressure term in Euler Number is replaced by difference in pressure at any two points in system.

The drop in pressure in pipe is most often sought for value in engineering study in which fluid is flowing. Therefore, the interdependence of dimensionless groups which may characterize a particular flow (say forced flow), then Eu = f [R_e]. This functional relationship holds for all similar steady-state processes but function itself is to be determined experimentally.