Module 3. Dimensional analysis and heat transfer

Lesson 14

TREATMENT AND GENERALIZATION OF TEST DATA, LOGARITHMIC MEAN TEMPERATURE, DIFFERENCE REFERENCE DIMENSIONS, REFERENCE TEMPERATURE

14.1  Treatment & Generalization of Test Data

14.1.1  Averaging fluid temperature

In the process of heating and cooling fluid temperature differ at different temperature points. It varies both over the cross section and along the length of the conduit. In engineering calculation we usually deal with mean fluid temperature and the average is calculated by a definite way, for specific problems.

14.1.1.1  Averaging over the cross section

Where = Total heat carried by the fluid

= Heat capacity of the fluid.

If the dependence on r and c_p on the temperature is ignored, the formula can be simplified:

Where v = volumetric rate of flow (m³/sec)

Further if the velocity of the fluid does not change over the cross section. The formula can be further simplified:

Now,

- In the first case averaging is based on enthalpy of fluid.

- In the 2^nd case it is based on the volumetric flow rate of the fluid.

- In 3^rd case, averaging is based on the cross section of the conduct.

14.1.1.2  Averaging based along the length of the conduit

In the process of heating and cooling the temperature of the fluid also varies along the length of the conduit. The mean temperature of the fluid along the length of the fluid can be determined as the arithmetic mean of the two extreme values.

But this averaging method is confined to those cases where the temperature varies but little along the length of the conduit. Therefore, in other cases averaging is done by:

Where,

t_w = Wall temperature

∆t = Logarithmic mean temperature difference.

This is defined as:-

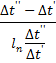
Where

 = Temperature difference for cold fluid

 = Temperature difference for hot fluid.

14.1.2  Reference temperature

Since the temperature of the fluid changes in the process of heat transfer, its physical property also changes. Therefore, it is very important for the investigator either to average the physical properties or to choose the temperature which may be referred as reference temperature. Therefore, in heating test data on heat transfer and pressure drop one should regard as reference temperature either the temperature given for engineering calculation or the temperature which can be easily determined.

14.1.3  Reference dimension

The reference dimension is also of great importance for the generalization of experimental data on heat transfer. For the presentation of the data in dimension less form, the reference dimension of a round tube is its diameter and for conduits of irregular and complex cross section, the reference dimension is the equivalent diameter which is equal to four times the cross sectional area of the conduit divided by wetted perimeter. In case of a plate, reference dimension is the length of the plate in direction of flow of heat in fluid.

14.1.4  Empirical formulas in the dimensionless forms

To extend the result of any individual experiment to the similar processes, the test data may be treated in dimensionless terms.