Module 3. Dimensional analysis and heat transfer

Lesson 19

PROBLEM ON FORCED CONVECTION (CONTINUED)

Q. 1. A thin plate of length l₀ = 2 m and width α = 1.5 m is exposed to a flow of air parallel to its surface. The velocity and temperature of the free-stream flow of air are respectively w₀ = 3 m/s and t₀ = 20°C. The temperature at the surface of the plate t_w = 90°C. Determine the lengthwise mean local coefficient of heat transfer from the plate to the air and the amount of heat transferred.

Solution:

For the air at a temperature t₀ = 20°C, ν = 15.06×10^-6 m²/s,  λ = 2.59×10^-2 W/m-°C,  Pr =  0.703. The Reynolds number

Consequently, in the boundary layer the pattern of flow is laminar. Under these conditions the lengthwise mean local coefficient of heat transfer from the plate to the air can be calculated from formula

Where

And the physical properties are selected for the temperature of the free-stream flow t_0.

In the case considered

And the local heat-transfer coefficient

The amount of heat transferred from the both sides of the plate

Q. 2. A flat plate of length l=1 m is exposed to air flow parallel to its surface. The velocity and temperature of the free steam air flow ω₀ = 80 m/s and t₀ = 10°C. A turbulizing grid is placed upstream of the plate, resulting in that the fluid is in turbulent flow in the boundary layer over the whole length of the plate.

Calculate the mean local coefficient of heat transfer from the surface of the plate and the value of the local heat transfer coefficient on the back edge. Also calculate the hydrodynamic boundary layer on the back edge of the plate.

Solution:

With a temperature of the free-steam flow t₀ = 10°C the physical properties of air are: ν = 14.16×10^-6 m²/s, λ = 2.51×10^{-2 W}/m-°C

Reynold’s number

The pattern of flow in the boundary layer on the plate is turbulent

With the plate exposed to air flow the mean heat-transfer coefficient for the turbulent boundary layer can be calculated from the following formula

N_u = 0.032 Re^0.8

Substituting the obtained value of the Reynold’s number into

For the plate in a longitudinal air flow with a turbulent boundary layer the local heat-transfer coefficient can be calculated from the following formula

where ^.

The value of the local coefficient of heat transfer on the back edge of the plate can be found, assuming x = l₀; then Re_𝓍 = 5.65 × 10⁶, Nu_𝓍 = 0.255(5.65 × 10⁶)^0.8 = 6280 and

The local thickness of the turbulent hydrodynamic boundary layer can be calculated from the formula

Substituting the value of the known quantities, we obtain at x = l₀:

Q. 3. Water flows along a tube of diameter d = 6 mm with a velocity w = 0.4 m/s. The temperature of the tube wall t_w = 50°C. What should the length of the tube be to ensure a water outlet temperature t_f2 = 20°C at a water inlet temperature t_w1 = 10°C?

Solution

The lengthwise mean temperature of water

The kinematic viscosity of water v_f = 1.16 × 10^-6 m²/s and the Reynold’s number

The pattern of water flow is laminar. At a reference temperature

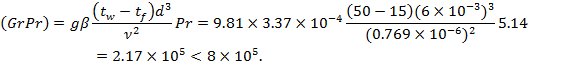
Consequently, the water is in viscous flow and to determine the local coefficient of heat transfer let us use formula. Since the relative length of the tube is not known, the problem must be solved by the method of successive approximations.

Let us assume a relative length of the tube l/d = 100 and consequently,

The physical properties of water are as follows:

Peclet number at the reference temperature

The correction for the section of hydrodynamic stabilization

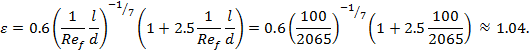
Nusselt number at the reference temperature

The heat-transfer coefficient

The amount of heat transferred through the wall

Where c_pf is taken based on the mean temperature of the fluid the c_pf = 15°C. On the other hand, the amount of heat transferred

Thus, after the first approximation we find

For the second approximation we select l=0.75 m, repeat the calculation and obtain:

After the second approximation we get:

Since the assumed length of the tube coincides with a sufficient accuracy with the result obtained after the second approximation, there is no need of the third approximation, and we may assume a length of the tube l = 0.76 m.