Module 4. Radiation heat transfer

Lesson 23

STEFAN-BOLTZMANN LAW, KIRCHOFF’S LAW, LAMBERT’S COSINE LAW

23.1  Stefan-Boltzmann law

The full amount of energy emitted per square meter of a black body per hour is

Integrating equation

 [Kcal/m²-hr]

Here  is the radiation constant of a black body, equal to 4.9 x 10^-8 kcal/m²-hr-°K⁴, according to latest data. The equation is the mathematical expression of the Stefan- Boltzmann law. In engineering calculations, this law is used in the following, more convenient, form:

Where C₀ is known as the Stefan-Boltzmann constant; C₀= 𝜎₀ × 10⁸ = 4.9 kcal/m²-hr-°K⁴. Hence, radiation energy is proportional to the fourth power of absolute temperature. The Stefan- Boltzmann law strictly applies only to an ideal radiator-a black body. Stefan and other investigators, however, have shown by experiment that this law is applicable to gray bodies as well. In this case, it acquires the following form:

The radiation factor C is different for different bodies. It depends on the nature of the body, the state of its surface and temperature; C is always smaller than C₀ and may range from 0 to 4.9.

Comparing the radiation energy of a gray body with that of a black body at the same temperature, we get another characteristic of the body called the relative radiant power or emissivity ε:

.

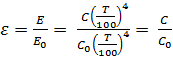23.2  Kirchhoff’s law

Kirchhoff’s law establishes the relationship between the emissivity and the absorptivity of a body. This relationship may be obtained by studying radiant interchange between two surfaces.

Consider two surfaces, one gray and the other absolutely black. The surfaces are arranged parallel to each other and so close that the radiation of each impinges upon the other. The temperature, emissive power and absorptivity of the surfaces are, respectively, T, E, A and T₀, E_o, A_o; A₀ = 1 and T>T₀. Let us write the energy balance for the gray surface. A unit area of the gray surfaces emits per unit time a certain amount of energy E [kcal/m²-hr]. The energy impinging upon the black surface is fully absorbed by it. In its turn, the black surface emits E₀ [kcal/m²-hr]. A portion AE₀ of this energy is absorbed by the gray body, and the remaining portion, equal to (1-A) E₀, is reflected and fully absorbed by the black surface. Thus, for the gray surface the energy input is AE and expenditure E. Consequently, the balance of radiant interchange is

E_res= q= E-AE₀ [kcal/m²-hr].

Radiant interchange between two surfaces also takes place when T = T₀. In this case, the system is in mobile thermal equilibrium and q = 0. Then, from equation we have

The relationship is applicable to any body and therefore may be rewritten as follows:

.

In this form, Kirchhoff’s law is formulated thus: For all bodies the ratio of the emissive power to absorptivity is the same and is equal to the emissive power of a black body at the same temperature, and depends only on the temperature.

From Kirchhoff’s law it also follows that the emissive power of bodies increases along with their absorptivity. If the absorptivity A of a body is low, its emissive power E is low too. Therefore, good reflectors are poor emitters; for instance, the emissive power of an absolutely white body is zero.

23.3  Lambert’s law

The Stefan-Boltzmann law determines the energy emitted by a body in all directions. Each direction is determined by the angle  which the emitted rays form with the normal to the surface. Lambert’s law defines the variation of radiation in individual directions. According to this law, the rate of radiation from surface element dF₁, in the direction of surface element dF₂ is proportional to the rate of radiation along the normal dQ_n multiplied by the solid angle d and cosi.e. (Fig. 23.1)

d cos[kcal/hr]

Or

d cos[kcal/hr]