Module 4. Radiation heat transfer

Lesson 24

RADIANT INTERCHANGE BETWEEN SOLIDS

24.1  Radiant Interchange Between Solids

Knowing the laws of radiation, absorption and reflection, and also the dependence of radiation on direction, it is possible to derive calculation formulas for radiant interchange between solids. The problem may be approached in different ways. For a body taken by itself, the thing is to determine the rate of heat radiation into the surrounding medium. Writing the heat balance, we get

q₁= E_1eff – E_2eff = E₁-A₁ E_2eff [kcal/m²-hr]         ………(1)

where E₁= radiation of the body proper , kcal/m²-hr;

          E_1eff = E₁ + (1-A₁) E_2eff is the effective radiation of the solid, kcal/m²-hr;

          E_2eff = impinging effective radiation emitted from surrounding bodies, kcal/m²-hr.

The impinging radiant heat can be determined only by measurement with the aid of special instruments- radiation meters or actinometers.

This method of calculation is employed in cases where the temperature and the emissive power of the surrounding bodies are not known. In heat engineering, it is usually required to calculate the radiant interchange between bodies whose state of surface, size and temperature are known. These data permit determination of the quantity of heat emitted from both bodies by means of the Stefan Boltzmann law. In this case the essential thing is to take into account the effect of the shape and size of the bodies, relative position, distance between the bodies and their emissivity. (Fig. 24.1)

Radiant interchange is a complex process of multiple attenuated absorptions and reflections. Part of the emitted heat returns again to the emitter, thereby slowing down the process of radiant-heat interchange. By way of illustration, let us consider the turnover of radiant heat in the simplest case of radiant-heat interchange between two parallel surfaces. The temperature, emissive power and absorptivity of the surfaces are, respectively, T₁, E₁, A₁ and T₂, E₂, A_2.

The first surface emits

E₁.                                   ………(a)

Of the emitted heat E₁ the second surface absorbs

E₁A₂ ……… (b)

And reflects   E₁ (1-A₂)                                                    ……… (c)

Of this, the first surface absorbs

E₁ (1-A₂) A₁                                                                        ……… (d)

And reflects

E₁(1-A₂)(1-A₁).                                            ……… (e)

The second surface again absorbs

E₁(1-A₂)(1-A₁)A₂.                                        ……… (f)

And reflects

E₁(1-A₂)²(1-A₁),                                             ……… (g) 

of which the first surface again absorbs

E₁(1-A₂)²(1-A₁)A₁….                                      ……… (h)

and so on ad-infinitum.

The same reasoning is applicable to the radiation of the second surface, namely, the second surface emits E₂; of this quantity of heat emitted, the first surface absorbs E₂A₁ and reflects E₂(1-A₁), etc. The considered process of radiant-heat interchange is graphically shown.

In order to determine the quantity of heat q₁₂ transferred by the first surface to the second by radiation, one has to subtract from the initially emitted heat E₁, first, the portion of heat reflected by the second surface and absorbed again by the first surface and, secondly, the portion of heat absorbed of the heat emitted by the second surface. The first subtrahend may be found by summation of the expressions (d), (h), etc.

E₁(1+p+p²+…) (1-A₂)A₁,                                   ……… (i)

where (1-A₂) (1-A₁) is assumed equal to p for convenience sake.

Since p<1, the sum of the infinitely decreasing geometric progression

1+p+p²+…=

Substituting this value in expression (e), we get

……….(j)

The second subtrahend may be written as follows:

……… (k)

From these expressions we find

……… (l)

    Reducing to the common denominator and taking into account that

,

we finally get

The same result is obtained if the effective radiation of surfaces is considered. According to equation no.1

 ……… (m)

where

and

        Solving the system (n) in respect to E_1eff and E_2eff we get

 ……… (o)

……… (p)

    Substituting the equation (o) and (p) in equation (m), we have:

      S B Law

According to equation,

and .

Substituting these values and rearranging the expression, we finally get

  [kcal/m²-hr],

where

and

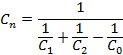
This is the calculation formula for radiant-heat interchange between two parallel surfaces. The factors A_n and C_n are called the reduced absorption and radiation factors of radiant-heat interchange between a system of bodies. Since A is numerically equal to ε, it may be replaced by ε.