Module 5. Heat exchangers

Lesson 26

MEAN TEMPERATURE DIFFERENCE, CALCULATING THE OUTLET TEMPERATURE OF WORKING FLUIDS

26.1  Mean Temperature Difference

In deriving the formula for the mean temperature difference, consider a parallel-flow heat exchanger of elementary design. The amount of heat transferred from the hot fluid to the cold fluid per hour through a surface element dF is determined from the following equation:

dQ = k(t1 – t2)x dF (kcal/hr).                                                                                                                                                                                                                       ………(a)

In the course of heat transfer the temperature of the hot fluid will decrease by dt1 and the temperature of the cold fluid increase by dt2.

Hence

dQ = -G1cp1dt1 = G2cp2dt2,                                                                                                                                                                                                                              ……… (b)

From which

image001                                                                                                                                                                                                                                ………(c)

image002                                                                                                                                                                                                                                 ………(d)

and the change in the temperature difference is equal to

image003                                                                                                                                                                              ………(e)

Where

Substituting the value of dQ from equation (a) into equation (e), we get

d(t1 – t2) = – mk(t1 – t2)x dF.                                                                                                                                                                                                                            ………(f)

Denoting the difference (t1 – t2)x by Δtx and separating the variables, we get

image005                                                                                                                                                                                                                                            ………(g)

If m and k are constant, integration of equation (g) gives

 Or

image007                                                                                                                                                                                                                                       ………(h)

From which

 =                                                                                                                                                                                                                                                 ………(i)

From equation (i) it is seen that along the heating surface the temperature difference or potential changes in accordance with the exponential law. Knowing this law, it is easy to determine the mean temperature difference ∆t. The theorem of the mean permits the following expression (at k = const) to be written:

image011                                                                                                                                                                      ………(j)

Substituting the values of mkF and e-mkF from equations (h) and (i) into equation (j) and bearing in mind that, according to the graph, ∆tx = Δt” at the end of the heating surface, we finally have

Or

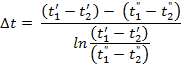
For a counter flow heat exchange, the only difference being that the right side of equation (d) must be taken with a minus sign and, consequently,

The final formula for the mean temperature difference of a counter flow arrangement has the following appearance:           

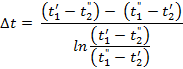
The arithmetic mean is always larger than the logarithmic mean. But at  the difference between the two means is less than 3 per cent. Such an error is fully admissible in engineering calculations.

Example. A chilled water tank is designed to cool hourly 250 l of hot liquid of gravity γ1 = 1,100 kg/m3 and heat capacity cp1 = 0.727 kcal/kg-°C, t’ = 120°C to t1" = 50°C. 1,000 l of water per hour is available for cooling purposes at a temperature t2’ = 10°C. Determine the required heating surface of parallel flow and counterflow apparatus, if k = 1,000 kcal/m2-hr-°C.

Solution: First let us determine the water equivalents W1 and W2:

            W1 = 0.250 X 1,000 X 0.727 = 200 kcal/hr-°C.

            W2 = 1 X 1000 X 1 = 1,000 kcal/hr-°C.

Δtʹʹ = 50-24 = 26°C;

For counterflow

;

;

The quantity of transferred heat is determined by formula

Q = G1cp1 () = W1 = 200 X (120-50) = 14,000 kcal/hr

Knowing Q and ∆t, it is easy to find the product kF by equation.

For parallel flow

For counter flow

Hence for parallel flow F = 240/1,000 = 0.24 m2 and for counter flow F = 218/1,000 = 0.22 m2.

26.2  Calculating the Outlet Temperature of Working Fluids

The goal of the calculations studied above was to determine the heating surface and principal dimensions of the heat exchanger for designing the apparatus in the future. Now consider a heat exchanger which already exists or has at least been designed. In this case, calculations aim at determining the outlet temperatures of the working fluids. Calculations of this kind are referred as checking calculations.

In a problem of this kind the following data are known: heating surface F, overall heat-transfer coefficient k, water equivalents W1 and W2 and inlet temperatures  and . The outlet temperatures  and  and the amount of transferred heat must be determined.

In approximate calculations one may depart from the following. The amount of heat lost by the hot fluid is equal to

Q = W1 () (kcal/hr),

From which the outlet temperature of the fluid  is determined by the relationship

image034                                                                                                                                                                                                                                                    ………(a)

And correspondingly for the cold fluid

Q = W2 () (kcal/hr),

And

image036                                                                                                                                                                                                                                                      ………(b)

Assuming the variation in the temperatures of the working fluids linear,

image037                                                                                                                                                                                                                                 ………(c)

Replacing the unknowns  and  by their values from equations (a) and (b), we obtain

image038                                                                                                                                                                                                                                   ………(d)

Further rearrangement of the equation gives

image039                                                                                                                                                                                           ………(e)

From which we finally get

           

Knowing the amount of transferred heat Q, it is very simple to determine the outlet temperatures of the working fluids  and  by formulas (a) and (b).

Although simple, this method of calculation is used only for approximate calculations and in cases of slight changes in the temperature of the working fluids. In general cases, the final outlet temperature depends on flow arrangement. Given below, therefore, is a method of deriving more precise formulas for parallel-flow and counter flow arrangements.