Module 5. Heat exchangers

Lesson 27

PARALLEL FLOW, COUNTER FLOW

27.1  Parallel Flow

It has been shown above that the change in the temperature difference follows the exponential law

Δt^” = Δt^’ e^-mkF

Knowing that

And that at the end of the heating surface Δt^” = , we substitute these values

This equation, however, shows only the temperature differences. It may be used to determine the individual outlet temperatures by subtracting both members of the equation from unity:

Inserting this value into the left side of equation, we obtain

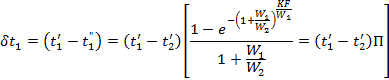
The latter equation shows that the change in the temperature of the hot fluid δt₁ is equal to a certain function Π of the initial temperature difference  and this fraction depends only on the two dimensionless terms and .

Processing in a similar way, we may derive the expression characterizing the change in the temperature of the cold fluid from formula

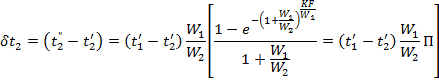
Having determined the variation in the temperature of the working fluids and knowing their inlet temperatures, it is easy to determine the final outlet temperatures:

The rate of heat transfer is determined by multiplying the water equivalent of the considered fluid by its change in temperature:

The function  is plotted in Fig. 27.1.

Example 2. Consider a water cooler with a heating surface F = 8 m². Determine the outlet temperatures of the fluids and the hourly rate of heat transfer Q for the following given data: V₁ = 0.25 m³/hr, γ₁ = 1,100 kg/m³, c_p1 = 0.727 kcal/kg-°C and  = 120°C. 1,000 l of cooling water a temperature = 10°C are available per hour. Besides, it is known that the overall heat transfer coefficient k = 30 kcal/m²-hr-°C.

            W₁ = 0.25 X 1,100 X 0.727 = 200 kcal/hr-°C.

            W₂ = 1 X 1000 X 1 = 1,000 kcal/hr-°C.        

The value of the function π is read off the graph (refer Fig. 27.1)

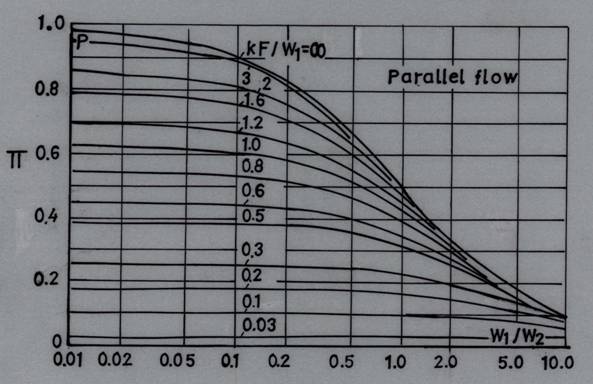
Fig. 27.1 -- auxiliary function used to calculate outlet temperature in parallel flow heat exchangers

The change (drop) in the hot fluid temperature is equal to

Hence the outlet temperature of the hot fluid is equal to

The amount of heat transferred per hour is determined by the expression):

The change in the temperature of the cold fluid is determined by equation), but it may also be found from the relationship Q = W₂ , from which

and .

27.2  Counter Flow

Calculation formulas for a counter flow arrangement are derived in the same way as for parallel flow. The final calculation formulas assume the following form:

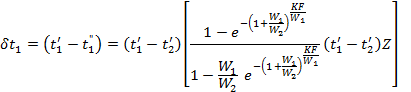
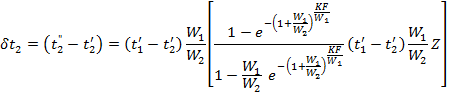
In a particular case where the formulas acquire the following form:

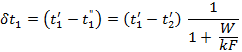
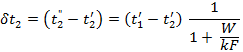
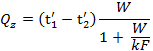
The function  is used to calculate outlet temperature in counter flow heat exchanger (refer Fig. 27.2).

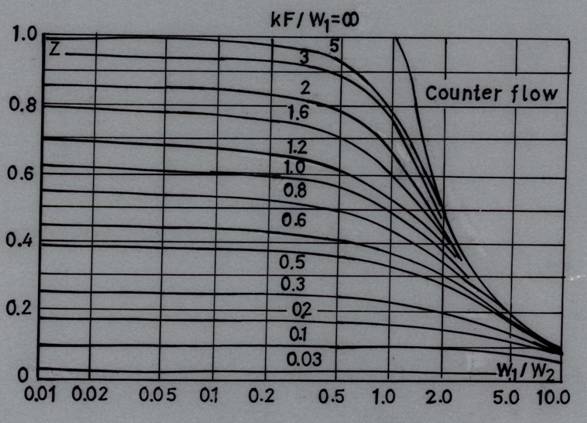
Fig. 27.2 -- auxiliary function used to calculate outlet temperature in counter flow heat exchangers

If the above formulas are used to calculate the temperatures of the working fluids and the amounts of heat transferred intermediate points of the heating surface, F is replaced by F_x; this is done only in the numerator and the value of the whole surface F is left in the denominator.