Module 2. Ideal gases
Lesson 3
LAWS OF IDEAL GASES: COMPRESSION AND EXPANSION OF GASES
3.1 Introduction
In the last chapter we studied the thermodynamic system containing working medium which is either a gas or vapor. Thermodynamic process is an energy exchange process and depends on the properties of working medium. Thus to know about the working medium, may be an ideal gas or a real gas or vapour, their properties and their behavior during energy exchange process is very important in thermodynamics.
3.2 Difference Between a Gas and Vapour
The gas is termed as the dry saturated or superheated state of a substance, in which the evaporation from liquid state is very much complete e.g. oxygen, nitrogen, air etc. at atmospheric temperature are considered as gases.
The vapors on the other hand may be defined as partially evaporated liquid i.e. the state of a substance, in which gaseous form consists of particles of liquid in suspension e.g. Wet Steam.
When these vapors are further heated, the remaining liquid particles also get evaporated at same temperature and on 100% evaporation, vapors becomes dry saturated.
On further heating the temperature of dry vapors increases and they become superheated. More and more, the vapors are superheated i.e. their temperature is increased beyond the evaporation temperature, their behavior approaches as that of a gas.
3.3 Ideal Gas
An ideal gas or a perfect gas is one which obeys all gas laws under all conditions of temperature and pressure. However, practically no gas is perfect because it does not strictly obey the gas laws.
However within the temperature limits of applied thermodynamics, many gases like hydrogen, oxygen and even air etc. may be considered as perfect gases.
3.4 Laws of Perfect Gases
Ideal gases or perfect gases are always considered to follow these laws while undergoing different thermodynamic processes.
3.4.1 Boyle’s law
It
states that the volume of a given mass of a gas varies inversely as its
absolute pressure, provided the temperature remains constant i.e.
![]()
Or ![]() ……… (Eq. 3.1)
……… (Eq. 3.1)
This is also shown in fig 3.1 as: Area 1-a-o-b = Area 2-c-o-d
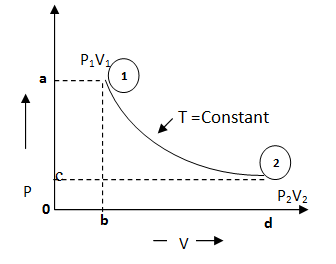
Fig. 3.1 Isothermal process
3.4.2 Charles’s law
It
states that volume of a given mass of a gas varies directly as its absolute
temperature provided the pressure is kept constant, i.e
![]()
![]() ………
(Eq. 3.2)
………
(Eq. 3.2)
3.5 Equation of State of a Perfect Gas
By combining the Boyle’s law and Charle’s law, the equation of state for a perfect gas can be derived.
For example: consider a perfect gas initially at a state of absolute pressure P1, absolute temperature T1 and specific volume v1. Let it be expanded or compressed at constant temperature to a new state of absolute pressure P2 and specific volume v1′. Then by Boyle’s law
P1v1 = P2 v1′ [Sub Eq. (i)]
Let after this
state, the gas is further expanded or compressed such that the pressure P2
remains constant. Let the new state is of specific volume v2 and absolute temperature T2.
Then by Charle’s Law:
![]()
![]() [Sub Eq. (ii)]
[Sub Eq. (ii)]
Now, putting the
value of v1′ in sub-equation (i)
![]()
![]()
![]()
Where, ‘R’
is known as characteristics gas constant.
Above equation can be re-written
as
![]()
![]() ………
(Eq. 3.3)
………
(Eq. 3.3)
It is called the equation of state of a perfect gas.
From the equation of state, the units of ‘R’ are J/ kg K.
For atmospheric air, value of ‘R’ is 287 J/ kg K.
3.6 Universal Gas Constant (Ru)
We know that one kg-mole of a gas is equal to M kg of the gas where M = molecular weight of gas
Let mass ‘m’ contains ‘n’ no. of kg moles, then m = n. M
From the
equation of state we know that
![]()
![]() ………
(Eq. 3.4)
………
(Eq. 3.4)
Now by Avogadro Law, equal volume of different perfect gases at the same temperature and pressure contain equal number of molecules or equal number of kg-moles. Thus by this rule if we see the equation of state given above for two different gases at same pressure, volume and temperature and so the same number of moles, the value of MR will also be same for these two gases. So the product of M & R, molecular weight and characteristics gas constant of any perfect gas is always constant and is named as universal gas constant (Ru).
It is found that Ru = M.R = 8314 J/ kg mole K
Thus equation of state can be re-written
in terms of number of kg moles as
![]() ……… (Eq. 3.5)
……… (Eq. 3.5)
This
is called as universal gas equation
3.7 Specific Heat
The specific heat of a substance is defined as the quantity of heat required to raise the temperature of a unit mass of the substance through a unit degree. It is denoted as ‘C’.
If the unit mass of substance is a gas then specific heat is of two types: as specific heat at constant pressure ‘CP’ and specific heat at constant volume, ‘Cv’.
Specific heat at constant volume, ‘Cv’ for a gas is the heat energy required to be supplied to unit mass of gas for unit degree rise in its temperature by keeping it at constant volume in a fixed volume container. While specific heat at constant pressure, ‘Cp’ for a gas is the heat energy required to be supplied to unit mass of gas for unit degree rise in its temperature by keeping it at constant pressure in a container, one boundary of which can move to allow for expansion of gas and hence to keep its pressure at a constant level.
CP is always more than CV and for a particular gas the ratio of CP and Cv i.e. γ (γ = CP/Cv) remains constant. By Regnault’s law, both types of specific heats remain constant with varying temperature and pressure. But this is only approximately true. In actual practice value of specific heats vary with varying temperature. Also for real gases CP & Cv increases considerably with increase in temperature.
Thus to calculate the quantity of heat exchanged only for a small temperature change, the following formula can be used
Q = m C Δt
Where, Q = Heat Exchanged
m = Mass of gas
C = Specific heat of gas
Δt = Temperature change of gas
Cp for air = 1.004 kJ/kg K
Cv for air = 0.7178 kJ/kg K
3.7.1 Molar specific heats
The molar specific heat of a substance is defined as the quantity of heat required to raise the temperature of one mole of a substance through a unit degree. Now the mass of one mole is M kg where, M is molecular weight of the substance.
Thus Cp-mol = M.Cp and Cv-mol = M.Cv
3.8 Compression and Expansion of Gases
When the volume occupied by a gas is shrinked or decreased by external means, the process is called compression of gas. If it is an ideal gas, it always follows the gas law or gas equation and the new value of its properties may be calculated by applying gas equation to new state. As the volume is decreased, pressure of gas increases and so temperature also increases. Thus external work is required against this increase in pressure, which actually is stored in the form of increased pressure and temperature of gas.
When some mass of gas is stored in a closed container at some higher pressure than its surroundings, it has ability to do some work through expansion. If any of the boundaries of system is movable or stretchable then gas inside at higher pressure may be able to move or stretch away this boundary against lower pressure of surroundings outside.
In this way volume occupied by gas will increase and so its pressure and temperature will decrease according to gas law. This process of increase in volume occupied by gas due to its own higher pressure is called expansion process (Fig. 3.2). During expansion, the internal energy and pressure energy of gas decrease and spent in the form of work energy at the movable or stretchable boundary of the system.
Thus it is either the compression or expansion process of a gas by which work is converted to heat energy or heat is converted to work energy.
3.9 Numerical Problems
3.9.1. Calculate the mass of air filled in a cylinder of volume 1 m3 and having 5 bar gauge pressure at a temperature of 27oC.
Solution:
Given that
Gauge pressure of air, Pg = 5 bar = 5 x 105 N/ m2
Volume of air = 1 m3
Temperature of air = 27oC
So, Absolute pressure of air = (5+1.013) bar
= 6.013 x 105 N/ m2
Absolute temperature of air = 27oC + 273 = 300 K
Also we know that characteristics gas constant of air, R = 287 J/ kg-K
Now
as per the equation of state of a perfect gas, ![]()
Putting given values in this
equation,
![]()
Answer: 6.98 kg
3.9.2. One m3 of a gas is compressed from its initial condition of 2 bar absolute pressure and 30oC temperature to final condition of 5 bar abs. pressure and 60oC temperature. What should be its final volume?
Solution:
Initial conditions of gas:
Absolute Pressure, P1 = 2 bar = 2 x 105 N/ m2
Absolute temperature, T1 = 30 + 273 = 303 K
Total volume of gas, V1 = 1 m3
Final conditions of gas:
Absolute Pressure, P2 = 5 bar = 5 x 105 N/ m2
Absolute temperature, T2 = 60 + 273 = 333 K
Total volume of gas, V2 =?
Perfect gas law is
![]()
Putting
the given values of initial and final condition :
![]()
Answer = 0.44 m3