Module 3. First law of thermodynamics

Lesson 4

FIRST LAW OF THERMODYNAMICS & NON FLOW PROCESSES

4.1 Introduction

The first law of thermodynamics is basically a form of law of conservation of energy i.e. energy can neither be created nor be destroyed and only it can be transformed from one form to the other.

It is actually a precise statement of law of conservation of energy in particular reference to heat energy and work energy which are our subject of study in thermodynamics. So whenever a thermodynamic system undergoes a thermodynamic process or cycle first law of thermodynamics is always to be followed. This law actually justifies or gives answer to any difference coming between heat exchange and work exchange of a system. Thus the calculation of any energy exchange in a thermodynamic process or cycle is based on this law.

4.2 First Law of Thermodynamics

4.2.1 Applied to a thermodynamic cycle

It states that when a system undergoes a cycle, then the net heat supplied to the system from its surroundings is equal to net work done by the system on its surroundings or net work done on the system is equal to the net heat rejected by the system.

i.e. ………(Eq. 4.1)

or Cyclic Integral of Heat Exchange = Cyclic Integral of Work Exchange

Corollary

A device or machine is impossible, which can produce work continuously without absorbing energy from its surroundings.

4.2.2 Applied to a thermodynamic process

If the first law is applied to a thermodynamic process in which initial and final state of the system are different, then it can be stated that the net heat exchange between system and surroundings is equal to the sum of net work exchange between system and surrounding and change in its internal energy (U).

Or Q = W + ∆U ……….(Eq.4.2)

Heat Exchanged in a process = Work Exchange + Change in Internal Energy

As shown in figure 4.1, the quantity Q is taken as positive if the systems absorbs or takes heat from its surroundings and negative if the system rejects heat to the surroundings. Unlike to that, the quantity W is taken as positive if the system is doing work on its surroundings and negative if the work is being done on the system by some external agency. The quantity ∆U, change in internal energy of the system is taken as positive or negative depending on its increase or decrease.

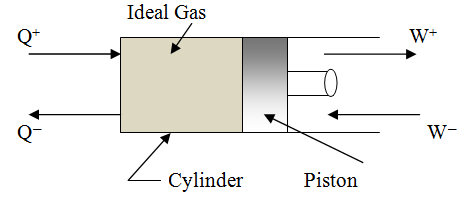
Fig. 4.1 Closed System

For a cycle, initial state is same as final state and as internal energy is a point function depending on state only, so net change in internal energy in a complete cycle is zero.

By putting ∆U = 0 in equation 4.2, it is reduced to equation 4.1 which is applicable to a cycle.

4.3 Internal Energy (U)

It has already been discussed in the first chapter that the internal energy is a property of the system and depends on temperature only. From the first law of thermodynamics as discussed in previous article

Q = W + dU

If there is a case when heat is supplied to a fix volume of gas (thermodynamic system) confined in fix boundary of the system i.e. there is no change in volume of gas during supplying of heat, then there will not be any work. So

W = 0 and dU = Q

As Q is heat supplied to gas keeping it at constant volume, it can be calculated as mC_vdt. Thus change in internal energy is heat exchanged at constant volume and can be calculated as

Change in internal energy per unit mass i.e.

……… (Eq. 4.3)

Thus internal energy is a property derived from first law of thermodynamics. It accounts for the difference between heat exchange and work exchange and shows that energy cannot be created nor be destroyed. Change in specific internal energy of a system is always calculated as C_vdt i.e. as a function of temperature change.

4.4 Enthalpy (H)

It is also a property of thermodynamic system which is calculated in terms of other properties. It is defined as the sum of internal energy and product of pressure and volume of a thermodynamic system. Thus it is a calculated property and loosely defined as total heat content of the system. It is denoted by ‘H’.

H = U + PV

And dH = dU + d (PV)

dH = dU + P.dV + V. dP

Enthalpy like internal energy is also a mass dependent property and enthalpy per unit mass is named as specific enthalpy and denoted as ‘h’.

Where m = mass of the system

If we consider a fixed mass ‘m’ of a gas confined in closed boundaries and remaining at constant pressure P, while absorbing heat Q. The temperature of gas will increase and simultaneously it will expand from initial volume V₁ to final volume V₂. So, by ‘first law of thermodynamics’.

Q = W + ∆U

mC_p(T₂– T₁) = (U₂ – U₁) + P(V₂ V₁) ……… (i)

Also enthalpy change during this constant pressure process 1- 2

= (U₂ – U₁) + P(V₂ V₁) ……… (ii)

[∴ P₁=P₂ in constant pressure process]

From (i) & (ii)

………(Eq. 4.4)
Thus change in enthalpy is also dependent on temperature only and is always calculated as C_p∆T.

4.5 Non-Flow Reversible Processes (Heating/Cooling and Expansion/Compression of Gases)

Until now we have studied that thermodynamic system of a gas is used to convert heat energy into work energy or vice versa which is required in a number of practical applications.

Thermodynamic system is also of many types. Here we will study a closed system which can exchange energy with surroundings but not the mass. Thus mass does not flow in or out of the system and so the processes of heating/cooling/compression/expansion etc are undergone by this fix mass of gas confined in continuous closed boundary are called Non-flow processes. In these processes some property of the gas may change and some may not change based on which a particular process is characterized. By applying first law of thermodynamics, the various forms of energy exchange can be calculated considering the processes as reversible i.e. taking all internal/external losses due to friction etc as nil.

For this let us consider a fix quantity of an ideal gas filled in a metallic cylinder as shown in fig. 4.2, one side of which is covered or fixed by a solid end plate and other side is covered by a moving piston. The outer wall of piston matches with inner wall of cylinder such that it makes a leak proof sliding joint. This moving piston makes one of the boundaries of system as moving or flexible.

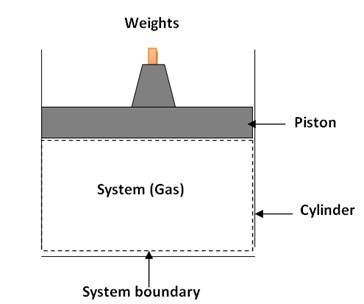
Fig. 4.2 Closed system of gas filled in metallic cylinder

When infinitely small heat ‘𝛅Q’ is supplied to gas from outside through the wall of cylinder, the gas tends to expand and forces the piston weight ‘F’ to move up. Let piston moves by a short distance, dl. Then the infinitesimal work done can be calculated as

= Pressure × Change in volume

Total work during a non-flow process 1-2 i.e. compression or expansion of gases can be calculated as taking integral of P.dV

……… (Eq. 4.5)

All these reversible processes of heat exchange (Heating or Cooling) and work exchange (compression or expansion) by a system of ideal gas with its surroundings can take place in various ways as discussed below:

4.5.1 Constant volume heating/cooling process

Let the piston is fixed at one point in the walls of cylinder such that volume V = Constant

So the ideal gas law PV/T = Constant will reduce to

Now let a small increment of heat 𝛅Q is supplied to the gas. As per 1^st law of thermodynamics

As V = Constant, 𝛅W = P.dV = 0

………(Eq. 4.6)

Thus knowing the values of 𝛅Q and C_v, ∆T (Increase in temperature) can be calculated and so ∆P can also be calculated from eqn 4.5. By measuring the small increment in temperature and pressure of system, the quantity 𝛅Q & ∆U can also be calculated.

4.5.2 Constant pressure process

Let the piston is free to move in the cylinder and force, F or pressure, P on the piston remains constant. So now the boundaries of the system can move and so the gas can expand or can be compressed i.e. the system is able to exchange work.

Now let a small quantity of heat, 𝛅Q is supplied to the gas through the walls of cylinder.

On absorbing this heat, the temperature of gas will tend to increase and simultaneously the gas will tend to expand against force F on the piston. Applying 1^st law of thermodynamic to this process.

or δQ = P.dV + mC_vdT ……… (Eq. 4.7)

or C_p = R + C_v

or C_p− C_v = R

Thus characteristic gas constant of an ideal gas is the difference between specific heat at constant pressure (C_p) and at constant volume (C_v).

The ratio of specific heats C_p/C_vis denoted as γ.

The physical meaning of R or γ can be taken as the characteristic of an ideal gas to expand under the influence of heat or we can say the increase in product of pressure and volume PV with increase in T.

Also by ideal gas law,

As pressure, P = Constant, the gas law reduce to V/T = Constant

Thus the increase in volume of gas due to expansion and increase in temperature are interrelated and if one can be measured the other can be found and the quantities W, ∆U and so Q can be calculated from equation 4.7 as

4.5.3 Constant temperature process (Isothermal Process)

The beauty of isothermal expansion or compression process is that the internal energy remains constant and so whole of the heat exchange by system is converted to work and vice versa. However the process is difficult to visualize while thinking that when the system (gas filled behind piston in the cylinder) absorbs heat, its temperature should always increase. But what happens in the isothermal process that while absorbing heat, simultaneously the gas expands thus decrease in its pressure and temperature takes place and the net change in temperature is zero. While expanding, the gas gives positive work equal to the heat supplied. Conversely also if the gas is compressed by doing extra work on the gas, its pressure and temperature tends to increase, but simultaneously if the gas is cooled in such proportion that the net change in temperature remains zero, the compression process becomes isothermal. In this isothermal compression process, again the work supplied to the gas is given away by the system in the form of heat.

Applying first law of thermodynamics to this isothermal process in which dU=0, because dT=0,

𝛅Q = 𝛅W = P.dV

……… (Eq. 4.8)