Module 3. First law of thermodynamics

Lesson 5

NON-FLOW AND FLOW PROCESSES

5.1  Non-Flow Processes

5.1.1  Adiabatic process

 Adiabatic process is one in which there is no exchange of heat between system and surroundings

 i.e.      Q= 0.

Applying first law of thermodynamics to this process

0 = δW + dU or δW = -dU

So,       dU = −δW = −P.dV                                                                                                                                                                                      ……… (Eq. 5.1)

Or in specific terms du = - δw = - P.dv   

 

Also from the definition of enthalpy, the change in specific enthalpy is

                                                                                                                                                                     ……… (Eq. 5.2)

Putting eq 5.1 into eq 5.2

dh = vdP

Thus in an adiabatic process

                                                                                                                                                                                              ……… (Eq. 5.3)

And     dh = CpdT = v.dP                                                                                                                                                                                           ……… (Eq. 5.4)

Dividing eq 5.4 by eq 5.3

           

or                                   

 

or

Integrating on both sides

or

or

=Constant

or

 

or

                                                                                                                                                                                                  ……… (Eq. 5.5)

This represents a reversible adiabatic process: 1-2

From gas law

or

                                                                                                                                                                                                                     ……… (Eq. 5.6)

or          

Putting the value of P1/P2 from equation eq 5.5



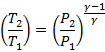
Thus the overall relation between initial and final properties (Pressure, volume and temperature) in an adiabatic process 1-2 is

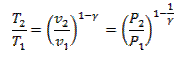                                                                                                                                                                          ……… (Eq. 5.7)

Work exchange

We know that work exchange during a non-flow process is given as

W=

Thus work during non-flow reversible adiabatic process 1-2 is

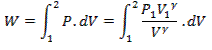                                                                                                                                                                                         ……… from (Eq. 5.5)

 

 

 

Specific work i.e. work per unit mass will be

                                                                                                                                                              ……… (Eq. 5.8)

If work exchange comes as positive that means gas is doing work on its surrounding during the process and if it comes as negative, the work is being done on the gas.

Also in the reversible adiabatic process 1-2, Q = 0 (no heat exchange) so as per first law of thermodynamics:

∆U = -W

Or

                                                                                                                                                                                                   ……… (Eq. 5.9)

5.1.2  Polytropic process

In real practice it is found that an ideal gas while undergoing a non-flow process which may be any one or combination of two of the heating / cooling and compression / expansion processes, follows the law.

PVn = Constant

Where ‘n’ is known as index of compression or expansion. (Fig. 5.1)

It is a general form of any non-flow process and the value of n decides the particular type of process. For example

·    If n = 0 ↔ then PV0 = constant Or P = constant

↔ constant pressure process.

·    If n = ∞  then PV∞ = constant

    or P1/∞.V = constant or P0V = constant or V = constant

↔ constant volume process 

·    If n = 1   then PV1 = PV = Constant.

              Mixing it with ideal gas law

            If PV = Constant, then T = constant

⟷ constant temperature process

·    If n = γ  then P = Constant 

↔ adiabatic process

·    If n has any other value except 0, 1, γ and ∞

↔ polytrophic process

Depending on the value of n, all these processes can be represented on the PV- diagram in Fig. 5.2 as follows.

Combining the polytrophic process law PVn = Constant with the ideal gas law


the relation between initial and final properties (pressure, volume and temperature) in a polytropic process1-2 can be derived as

                                                                                                                                                                                                                      ……… (Eq. 5.10)

5.1.2.1  Heat / work exchange

The difference in mathematical law governing an adiabatic and polytropic process is only of ‘γ’ and ‘n’. So work exchange in a polytropic process can also be similarly derived as in case of adiabatic process and it will be

And specific work,    

                                                                                                                                                                                                               ……… (Eq. 5.11)

 Applying first law of thermodynamics to the polytropic process 1-2                                               

Q = W + ∆U

           

           

           

                                                                                                                                                                                                                              ……… (Eq. 5.12)

5.2  Flow Processes

The processes which happen in an open system are called flow processes. As already studied, an open thermodynamic system is one in which there is not a fixed quantity or mass of gas/vapours but the working substance continuously flow in or out of the system. When this flowing substance or fluid exchange heat & work energy with the surrounding, the process is called flow process. Examples of this type of system are IC engines, centrifugal pump, steam turbines, water turbines etc. These flow systems may further be of the two types as steady flow system and unsteady flow system as discussed below:

5.2.1  Steady flow systems

The system through which the mass flow rate is constant i.e.

Mass Input = Mass Output

is a steady flow system. The state of working substance at any point in this system remains constant. Examples: Most actual thermodynamic equipment work as steady flow system under steady state conditions. Examples are IC engine, Compressors, steam turbines etc.

5.2.1.1  Analysis of steady flow system

Under steady state,    Total Inlet Energy = Total Outlet Energy

Now Total Energy = I.E. + F.E + K.E + P.E

 Where

                        I.E. = Internal Energy = mu

                        F.E. = Flow Energy = mPv

                        K.E. = Kinetic Energy = mV2

                        P.E. = Potential Energy = mgZ

So,    

 

In steady flow system the rate of mass flow is constant.

i.e.        Mass Input = Mass output

Or                      m1 = m2

 

Fig. 5.3 Open system

Also let the height of working substance at any point in the system remains constant. i.e.  

z1 = z2.

 And the kinetic energy is usually so small w.r.t. heat, work & enthalpy term, it can also be neglected.

Also taking U1 + P1V1 = h1 (enthalpy)

H1 + Q = H2 + W

Or        Q = dH + W                                                                                                                                                                                                    ……… (Eq. 5.13)

Or        dH = δQ – δW

Or        dU + P.dV + V.dP = dU + P.dV−dW

Or        V.dP = −dW

So work done in a flow process is given as                                                                                                                                         ……… (Eq. 5.14)

‘-ve’ sign indicates that work is ‘+ve’ during expansion i.e. when pressure decreases or dP is negative. And when during compression dP is positive, work will be negative.

5.2.2  Un-steady flow system

The open system through which the mass flow rate of working substance is not constant is un-steady flow system. Here the study of unsteady flow system is beyond the scope of syllabus. 

5.3  Internal Energy and Enthalpy of an Ideal Gas

We know that internal energy is the function of temperature only i.e. U = f (t)

To find that function use the relation for sp. heat at constant volume

As u is a function of temp only and ∂u/∂t is same for any pressure or volume and either one of them vary or remain constant.

Thus
                                                                                                                                                                   ……… (Eq. 5.15)

Thus the change in internal energy of an ideal gas for a particular change in temperature is always the same, whatever the process may be. For an ideal gas

sp enthalpy,    h = u + Pv

                          = u +RT            (for an ideal gas)

                          = f1 (t) + f2 (t)

So, specific enthalpy of an ideal gas is also a function of temperature only i.e.  

h = f (t)

To find this function use the relation for specific heat at constant pressure.


As the enthalpy is a function of temperature only for an ideal gas i.e. the change in enthalpy for a particular change in temperature is always the same irrespective of the type of process

So 
                                                                                                                                                                                                    ……… (Eq. 5.16)