Module 3. First law of thermodynamics
Lesson 6
NUMERICAL PROBLEMS
6.1 Numerical Problems
6.1.1 In an air motor, the compressed air, at internal energy 500 kJ/kg is expanded in the motor cylinder. During expansion, 130 kJ of heat per kg of air is rejected to the surrounding and work of 150 kJ/kg of air is done. What will be the final internal energy of air?
Solution
Given that
Specific Internal energy at beginning of expansion,
u1 = 500 kJ/kg
Heat rejected by air during expansion process
Q = -130 kJ/kg (-ve sign is there because heat is rejected)
Work done by air during expansion
W = 150 kJ/kg (expansion work is positive)
Applying first law of thermodynamics to the expansion process 1-2
Q = W + (u2-u1)
-130 = 150 + (u2 – 500)
Or
u2= 500-130-150= 220 kJ/kg
Hence final internal energy of air = 220 kJ/ kg (Ans.)
6.1.2 In an air compressor (reciprocating type), air is alternatively sucked & compressed by reciprocating piston in the cylinder. After one suction stroke, air is at a state of 105 Pa of pressure, 270C of temperature and 0.86 m3/kg of specific volume. If it is compressed to a final pressure of 6 x 105 Pa and compression process is assumed as isothermal. Determine: (i) Work done; (ii) Change in internal energy; (iii) Heat transferred.
Solution
Let the isothermal compression process of air is from state 1 to state 2.
Initial State 1 is given as:
Absolute Pressure, P1 = 105 Pa
Absolute temperature, T1 = 27 + 273 = 300 K
Specific volume, v1 = 0.86 m3/kg
As the process is isothermal so final temperature is same as initial temperature
i.e. T2 = T1 = 300 K
Find pressure, P2 = 6 x 105 Pa
Also during isothermal process
PV
= Constant or P1V1 = P2V2 for an
ideal gas
![]()
Applying first law of thermodynamics to this reversible non-flow isothermal process in which change in internal energy is zero.
Q = W + ∆u
Or Q = W ……… (i) (∆u = 0 in isothermal Process)
![]()
![]()
![]()
![]()
![]()
(-ve sign indicates that work is done on the air.)
Thus work done on the air =154 kJ/kg (Ans.)
Also heat transferred,
Q = W = -154 kJ/kg (-ve heat transferred means heat is rejected by air.)
Thus heat rejected by air = 154 kJ/kg (Ans.)
6.1.3 One kg of a perfect gas is compressed from an initial state of 1 bar pressure and 25oC temperature to a final pressure of 6 bars. The index of compression, n=1.25. Considering the process as reversible, determine: (i) Change in internal energy; (ii) Compression work; (iii) Heat transferred by gas. Given that molecular weight of gas = 30; Specific heat of gas at constant pressure, CP = 1.7 kJ/kg K
Solution
Given that:
Mass of gas, m=1kg
Initial Pressure, P1 = 1 bar = 105Pa
Final Pressure, P2 = 6 bar = 6×105Pa
Initial temperature, T1 = 25 + 273 = 298 K
Index of compression, ‘n’ = 1.25
So Law of polytropic compression is PV1.25 = Const.
Ru = 8314 J/kg K (Universal Gas Constant)
Mol.
Weight, M of gas = 30
So, the characteristic gas constant is equal to
![]()
Also Cp is given = 1.7 KJ/kg K=1700J/kg K. So
Cv = Cp – R
= 1700-277.13
= 1422.86J/kg K
![]()
We
know that during a polytropic process 1-2 the relation between initial &
final properties is as
![]()
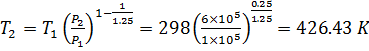
Change in Internal Energy
We know that change in internal energy during a process 1-2 is calculated as
U2-U1= mCv(T2-T1)
![]()
Thus increase in internal energy of gas = 182.736 kJ (Ans.)
Compression Work
In
a reversible polytropic process, work exchange is calculated as
![]()
![]()
![]()
![]()
-ve sign indicate the work is done on the gas. So, compression work = 142.367 kJ
Heat Transferred by gas:
By first law of thermodynamics
Q = W + ∆U= -142.367 + 182.736 = 40.37 kJ
As
this quality is positive so heat is absorbed by gas and is equal to 40.37 kJ
(Ans.)
6.1.4 In an air compressor, air flows steadily at the rate of 0.2 kg/s. The condition of air at the inlet of compressor is given as: pressure = 0.9 bars; specific volume = 0.9 m3/kg; flow velocity = 5 m/s and temperature = 15oC. The condition of air at the discharge point is measured as 7.2 bars with specific volume of 0.2 m3/kg, temperature 225oC and flow velocity 4m/s. Heat taken away by cooling water from the compressor cylinder is 30 KJ/s. Calculate the power required to derive the compressor. Take specific heat at constant volume, CV for air =717 J/kg K
Solution
Given data is
Air mass flow rate in the compressor, m= 0.2 kg/s
Velocity of air at the inlet of compressor, C1 = 5 m/s
Velocity of air at the outlet of compressor, C2 = 4 m/s
Pressure of air at the inlet of compressor, P1 = 0.9 x 105 Pa
Pressure of air at the outlet of compressor, P2 = 7.2 x 105 Pa
Specific volume of air at the inlet to compressor, v1=0.9 m3/kg
Specific volume of air at the outlet to compressor, v2=0.2 m3/kg
Temperature of air at the inlet to compressor, T1 = 15 + 273=288K
Temperature of air at the outlet to compressor, T2 =225 + 273=498K
Heat rejection rate of compressor = 30 KJ/s = 30/0.2 = 150 kJ/kg
Power required to derive the compressor
Using the steady flow energy equation:
![]()
![]()
![]()
![]()
![]()
(-ve
sign means work will be done on the air to compress it)
So, the power required to compress 0.2 kg of air per second will be
P = 63565.5 x 0.2 =12713 J/s = 12713 W or 12.713 kW (Ans).
6.2 Unsolved Problems
6.2.1 A closed system of constant volume experiences a temperature rise of 200C when a certain process occurs. The heat transferred in the process is 18 kJ. The specific heat at constant volume for the pure substance comprising the system is 1.2 kJ/ kg 0C, and the system contains 2 kg of this substance. Determine the change in internal energy and the work done.
[Ans. ∆U = 48 kJ; W = -30 kJ]
6.2.2 A
stationary mass of gas is compressed without friction from an initial state of
2 m3 and 2 × 105 N/m2 to
a finial state of 1 m3 and 2 × 105 N/m2, the pressure remaining
the same. There is a transfer of 360 kJ of heat from the gas during the
process. How much does the internal energy of the gas change?
[Ans. ∆U = -160 kJ]
6.2.3 A system receives 42 kJ
of heat while expanding with volume change of 0.123 m3 against an
atmosphere of 12 N/ cm2. A mass of 80 kg in the surroundings is also
lifted by a distance of 6 meters.
i. Find the change in energy of the system.
ii.
The system is returned to its initial volume by an adiabatic
process which requires 100 kJ of work. Find the change in energy of the system.
iii.
Determine the total change in energy of the system.
[Ans. (i) 22.54 kJ, (ii) 100 kJ, (iii) 122.54 kJ]
6.2.4 In the compression stroke
of an internal-combustion engine, the heat rejected to the cooling water is 45
kJ/ kg and the work input is 90 kJ/ kg. Calculate the change in internal energy
of the working fluid stating whether it is a gain or loss.
[Ans. 45 kJ/kg (gain)]
6.2.5 85 kJ of heat is
supplied to a system at constant volume. The system rejects 90 kJ of heat at
constant pressure and 20 kJ of work is done on it. The system is brought to its
original state by adiabatic process. Determine the adiabatic work done. Determine
also the value of internal energy at all end states if initial value is 100 kJ.
[Ans. W = 15 kJ; U1 = 100 kJ, U2 = 185
kJ, U3 = 115 kJ]
6.2.6 An air compressor takes
in air at 105 Pa and 270 C having volume of 1.5 m3/kg
and compresses it to 4.5 × 105
Pa. Find the work done, heat transfer and change in internal energy if the
compression is isothermal.
[Ans. -225 kJ; -225 kJ; ∆U =0]
6.2.7 A cylinder fitted with
piston contains 0.2 kg of N2 at 100 kPa and 300C. The
piston is moved compressing N2 until the pressure becomes 1 MPa and
temperature becomes 1500 C. The work done during the process is 20
kJ. Determine the heat transferred from N2 to the surroundings. Take
Cv = 0.75 kJ/kg K for N2
[Ans. -2 kJ]
6.2.8 The specific heat at constant pressure
of one kg fluid undergoing a non-flow constant pressure process is given by
![]()
Where, T is in 0C.
The pressure during the process is maintained at 2 bars and volume changes
from 1 m3 to 1.8 m3 and temperature changes from 500C
to 4500C. Determine
(i)
Heat
added
(ii) Work Done
(iii) Change in internal
energy
(iv) Change in enthalpy.
[Ans. (i) 1076 kJ ; (ii) 160 kJ ; (iii) 916 kJ ; (iv) 1076
kJ]
6.2.9 Air at 1.02 bar, 220
C, initially occupying a cylinder volume of 0.015 m3, is compressed
reversibly and adiabatically by a piston to a pressure of 6.8 bar. Calculate:
(i)
The final
temperature
(ii) The final volume
(iii) The work done on the mass of air in the cylinder.
[Ans. (i) 234.50C, (ii) 0.00388 m3,
(iii) 2.76 kJ]
6.2.10 One kg of a perfect gas
is compressed from 1.1 bar, 270 C according to a 1aw pv1.3
= constant, until the pressure is 6.6 bar. Calculate the heat flow to or
from the cylinder walls,
(i) When the gas is ethane (molecular weight 30), which has
Cp = 1.75 kJ/kg K.
(ii) When the gas is argon (molecular weight 40), which has
Cp = 0.515 kJ/kg K.
[Ans. (i) 84.5 kJ/kg, (ii) -59.4 kJ/kg]