Module 4. Second law of thermodynamics

Lesson 7

SECOND LAW OF THERMODYNAMICS, ENTROPY, CARNOT CYCLE

7.1  Introduction

In the last chapter we studied that heat and work are different forms of energy and are convertible in to each other. During this conversion, law of conservation of energy i.e. first law of thermodynamics is followed. But this law has limitation in depicting the fraction of heat energy of a system or supplied to system which can be converted to work. Also it does not specify the conditions under which conversion of heat in to work is possible. Second law of thermodynamics removes this limitation and tells under what conditions, in what direction of heat flow and how much of it can maximum be converted in to work.

7.2  Statements of Second Law of Thermodynamics

7.2.1  Kelvin-Planck statement

“It is impossible to construct a thermodynamic system or device which operates in a cycle and produce no effect other than the production of work by exchange of heat with a single reservoir”. Or in simple terms it states that all the heat from a single heat reservoir cannot be converted to work.

In detail, the meaning of statement is that there is no such device possible which can continuously take heat from heat reservoir on one side and convert all of it into work on the other side. But only a part of heat energy while flowing from high temperature reservoir to low temperature reservoir can be converted to work and the remaining part must be rejected to low temperature reservoir i.e. atmosphere. Therefore only a part of heat energy while in transition from high temperature to low temperature is possible to be converted in to work.

7.2.2  Classius statement

This statement is regarding the conversion of work in to heat and it states that (“it is impossible to construct a thermodynamic system or device which, while operating in cycle (i.e. working continuously), transfers heat from low temperature reservoir to high temperature reservoir without taking help or absorbing work from some external agency.)

In detail, the meaning of statement is that heat can be made to flow from low temperature to high temperature only by applying external work.

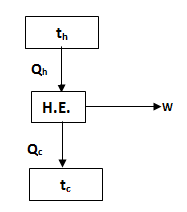
7.3  Heat Engine

It is a thermodynamic system or device which can continuously convert heat energy into work energy or we can say thermal energy in to mechanical energy. We know that to work continuously, anything has to operate in a cycle. Therefore heat engine is also a thermodynamic device operating in a cycle. The performance of a heat engine is measured in terms of its thermal efficiency which is the ratio of work output to heat absorbed by engine, i.e.

 

Where W = Rate of mechanical work done by engine

Q = Heat absorbed by engine or rate of heat supplied to engine.

7.3.1  Reversible heat engine

A heat engine which operates through a reversible cycle is called Reversible Heat Engine. As per second law of thermodynamics, heat engine absorbs heat Qh from a high temperature source, converts a part of it into Mechanical work ‘W’ and rejects the remaining part of heat ‘Qc’ to a low temperature heat sink as shown in Fig. 7.1. If the heat engine is reversible i.e. all its processes are reversible, then it can be operated on the reverse cycle in reverse direction with the same performance. Then it will start taking heat ‘Qc’ back from low temperature heat source by absorbing same amount of work ‘W’ from some external agency and reject the sum of heat absorbed and work absorbed in the form of heat ‘Qh’ to high temperature heat source. This reversed heat engine will be called heat pump as shown in Fig. 7.1. If this heat pump is used for the purpose of extracting heat from a low temperature body, it is called a refrigerator.

7.3.2  Corollary of 2nd law of thermodynamics

No heat engine operating between two heat reservoirs, always operating at constant temperature, can be more efficient than a reversible heat engine operating between the same temperature limits. Also all types of reversible heat engines operating between same temperature limits will have the same efficiency. It can also be proved with a simple logic. Let us say, there is an irreversible engine having more efficiency than that of a reversible engine operating between same temperature limits. Let irreversible engine produces work ‘W’irr and reversible engine produces work Wrev (such that Wirr>Wrev) by absorbing heat Qh from heat source at temperature Th and rejecting heat Qc to heat reservoir at temperature Tc. Now if we operate reversible engine in reverse direction like a heat pump taking work ‘Wrev’ from the work produced by irreversible engine and absorbing heat Qc back from heat reservoir at temperature Tc and rejecting back heat Qh to heat reservoir at temperature Th as shown in fig 7.2. We will find that a net positive work, W = Wirr - Wrev should be produced continuously without any effect or any net heat exchanged with reservoirs which is completely opposite to the law of conservation of energy i.e. energy cannot be produced without its expenditure.

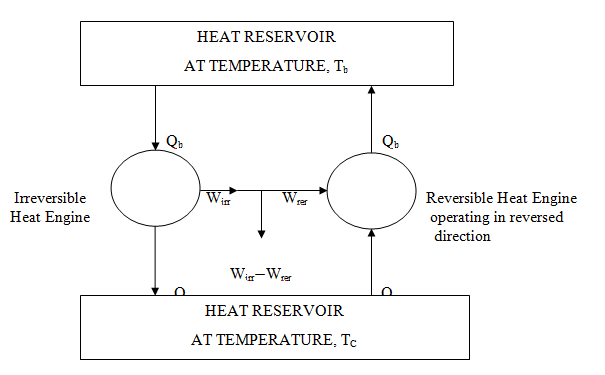
Fig. 7.2 Reversible and irreversible heat engines

In this way, our assumption that an irreversible engine is more efficient than a reversible engine is totally wrong. Hence

Wrev > Wirrev

One more fact about a reversible heat engine is that it does not exist in reality. But the idea of reversible heat engine is completely hypothetical in which the heat exchange process is thought as reversible without any change in temperature. Otherwise heat exchanged in a medium is irreversible and taken as Q = m.C.ΔT,

m = mass

C = Specific heat

ΔT = temperature change.

When some heat flows from a high temperature body to low temperature body, change in their temperatures occurs i.e. hot body becomes somewhat cool and cool body becomes somewhat hot, but now this heat cannot come back from cold body to hot body i.e. it is an irreversible process.

So, with ΔT = 0 i.e. heat exchanged without change in temperature can only be visualized in a way that the heat reservoirs and working medium in the reversible heat engine, which is exchanging heat with heat reservoirs, both are of infinite heat capacity and there is no change in their temperature and the amount of heat exchanged depends on the absolute temperature of reservoirs at which heat is being exchanged i.e. Q ∝ T. So in a reversible heat exchange process happening at constant temperature, heat exchanged is proportional to absolute temperature. This is also named as CLASSIUS statement.

7.4  Carnot Cycle/Carnot Engine

Carnot suggested a reversible cycle comprising of two reversible isothermal heat exchange processes and two reversible adiabatic expansion/compression processes as shown on P-V and T-S charts in Fig 7.3 (a)

 

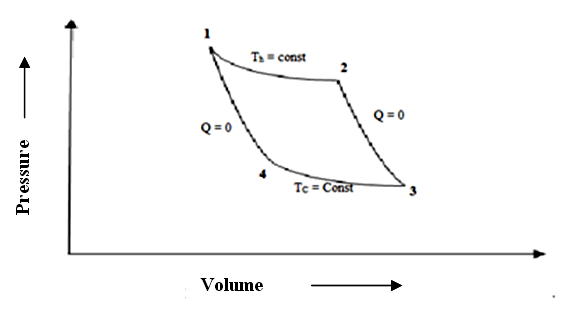
Fig. 7.3 (b) Carnot cycle

Carnot Engine is the reversible heat engine working on Carnot cycle 1-2-3-4 as explained below:

Process 1-2: Reversible isothermal heat addition: Heat, Qh is transferred to the working substance from the high temperature reservoir at temperature Th = T1 =T2. The heat transfer is reversible and isothermal. Expansion of gas takes places i.e. heat energy is converted to work but the internal energy of system remains constant.

Process 2-3: Reversible adiabatic expansion: During the expansion process, the system is thermally insulated so that Q = 0. The temperature of the working substance decreases from high temperature, Th to low temperature, Tc = T3 = T4. Expansion of gas takes place at the expense of its own internal energy.

Process 3-4: Reversible isothermal heat rejection: Heat Qc is transferred from the working substance (gas) to low temperature heat reservoir (sink) at constant temperature ‘Tc’. Heat transfer is isothermal & reversible. Gas is compressed by spending of external work and equivalent heat to this work is rejected to heat sink. Internal energy remains constant.

Process 4-1: Reversible adiabatic compression: During the compression process, the system is thermally insulated, so Q =0. Temperature of working substance increases from Tc to Th. So internal energy of the system increases by an equal amount to the compression work done on the system.

7.4.1  Carnot efficiency

An engine operating on the Carnot cycle has maximum efficiency.

                                                                                                                                            ……… (Eq. 7.1)

 Now,            Qh ∝ Th, Absolute temperature of hot reservoir

Qc ∝ Tc, Absolute temperature of cold reservoir

Thus,

                                                                                                                                                                 ……… (Eq. 7.2)

Thus, the Carnot efficiency does not depend on the type of working substance but only on the absolute temperature of hot & cold reservoirs.

7.5  Classius Equality & Inequality

As per corollary of 2nd law of thermodynamics all the reversible engines operating between two heat reservoirs at the same temperature, have the same efficiency, irrespective of the working substance used. That means between the temperature th & tc the value of Qh & Qc are always same for any reversible engine.

 

The function ‘f’ proposed by Kelvin and subsequently accepted is given by the simple relation.

                                                                                                                                                    ……… (i)

Where ‘C’ is a constant and Th & Tc are the absolute or thermodynamic temperatures on thermodynamic temperature scale.

Or

           

or

 

It is called Classius equality for a reversible cycle.

In case of an irreversible cycle for a heat engine,

Wirrev < Wrev

Or        Qh - Qirr < Qh – Qrev

(for the same amount of heat absorbed, Qh in both cases)

Or      Qc irr > Qc rev

Or       

 ,

which is called Classius inequality.

Thus Classius Equality and In- equality statements can be combined in mathematical terms as:

                                                                                                                                                                              ……… (Eq. 7.3) 

7.6  Concept of Entropy

As the first law of thermodynamics introduces a property named as internal energy. Second law of thermodynamics, when applied to a process, introduces the property named as entropy, which is of extensive type.

The physical significance of entropy is somewhat difficult to imagine, but if we start from the very basic, it will definitely give an idea of entropy and also its importance in thermodynamic calculations.

Now consider a reversible cycle “1A2B1” having two reversible processes A & B between the states 1 & 2 and another reversible cycle “1A2C1” having two reversible processes A and C between the same states 1 & 2, as shown in fig 7.4.

Fig. 7.4 Reversible cycles

Applying Classius equality to reversible cycles 1A2B1 and 1A2C1

 

From the above two equations:

Thus, we see that  for any reversible process between state 1 & 2 is same i.e. independent of path followed B or C or any other path (process) and depends only on states 1 & 2. Thus it is a point function and hence is a property called entropy (S), such that a change in this property,   Hence change in entropy during a process 1-2 is given as:

 

                                                                                                                                                                ……… (Eq. 7.4)

Thus, entropy of a system may be defined as a property such that change in it from one state to other is always equal to integral of heat exchanged divided by absolute temperature, at which heat is exchanged, during any reversible process between the states.

7.6.1  Specific entropy

Entropy per unit mass is called specific entropy. It is denoted by small letter ‘s’.

Conclusion: For a reversible process in a closed system

a)   Entropy increases if heat is added

b)  Entropy decrease if heat is rejected

c)   Entropy remains constant if there is no heat transfer.