Module 4. Second law of thermodynamics
Lesson 8
ENTROPY AND AVAILABILITY
8.1 Entropy Change for an Irreversible Process in a Closed System
First of all, it may be made clear here that, entropy is a property and any change in it between two states is always constant irrespective of the type of process between these states.
Let us consider a reversible cycle 1A2B1 formed by two reversible processes A and B between state 1 & 2 and an irreversible cycle 1A2C1 formed by one reversible process A and other irreversible process C between states 1 & 2 as shown in Fig 8.1.

Fig. 8.1 Irreversible cycle
Applying Classius equality & inequality to both cycle (1A2B1)rev & (1A2C1)irr
![]() (i)
(i)
![]() 0
(ii)
0
(ii)
From (i) and (ii)
![]()
It is due to ve
sign otherwise the numerical value of ![]() is
high.
is
high.
Now
![]()
Thus for the
irreversible process C, change in entropy
![]()
So even if Q =0 for irreversible process, the entropy will always increase. It can be taken mathematically as
![]()
Where, δI is the rise in entropy due to irreversibility factor
By integrating the total change in entropy during an irreversible process is
![]() (Eq. 8.1)
(Eq. 8.1)
The effect of this irreversible term I is always to increase some entropy whether the heat is added or rejected or not exchanged.
Conclusion
For an Irreversible Process
1. If heat is added, entropy increases due to heat addition and irreversibility.
2. If there is no heat transfer, the entropy still increases due to irreversibility.
3. If heat is rejected, entropy decreases due to heat rejection and increases due to irreversibly. Net effect may be +ve or ve.
General
mathematical statement for change in entropy between two states is
![]() (Eq. 8.2)
(Eq. 8.2)
Where
= sign is for Reversible process between the given states.
> Sign is
for Irreversible Process between the given states.
It can be understood more clearly with the help of fig. 8.2 as given below:

Fig.
8.2 Relationship of change in entropy with heat exchange during reversible and
irreversible processes
8.2 Carnot Cycle on Temperature- Entropy Chart
As the entropy is a property, it can be tabulated for a pure substance as a function of two other independent properties.
Also, as it is a property it can be plotted on a chart with another property. Most common charts that are used in thermodynamics are T-s charts. Area under the curve on T-s chart gives directly the heat added or rejected for a reversible process.
Thus Carnot cycle can also be represented more conveniently on a T-s chart because it is comprised of two isothermal (constant temperature) processes and two reversible adiabatic (constant entropy) processes. It is shown in Fig. 8.3 as 1-2-3-4. Four processes of Carnot cycle are as follows:
Process 1-2: Isothermal heat absorption. Heat absorption is given by area under line 1-2.
Process 2-3: Reversible adiabatic expansion Process, δQ = 0, so dS = 0
Process 3-4: Isothermal Heat Rejection. Heat rejection is given by area under line 3-4.
Process 4-1: Reversible adiabatic compression, δQ =0, so dS = 0
Heat Absorption, Qh = Th∆S (Area under line 1-2)
Heat Rejection, Qc = Tc∆S (Area under line 3-4)
So, Net work of cycle, W = Qh Qc = (Th-Tc) ∆S (Area covered by cycle 1-2-3-4 on T-S chart)
Thermal
efficiency of Carnot cycle is given as
![]()
Thus it is easier to draw, analyze the Carnot cycle and find its thermal efficiency on a T-S chart.
8.3 Availability
It is the work potential of any source of energy at some specified state. It is also referred to as exergy. It is represented as available energy, which is the maximum possible work that can be extracted from a heat source at temperature, Th by introducing a reversible heat engine taking heat from it and rejecting remaining heat to surroundings at temperature, Tc. (Fig. 8.4)
If Q is the amount of heat available with heat reservoir at temp Th, then
Available
Energy, A.E =
(![]() .
.
And Unavailable Energy, U.E = Q - A.E.
From fig 8.3
Area 1- 2- S1- S2, = Qh = Heat absorbed
Area 1-2-3-4 = W = Available Energy (A.E.)
Area----3- 4- S1- S2 = QC = Unavailable Energy (U.E.)
Thus,
![]() (Eq. 8.3)
(Eq. 8.3)
![]() (Eq. 8.4)
(Eq. 8.4)
If Th increases A.E increases & if Th decreases, A.E decreases. (Fig.8.5)
8.3.1 Real conditions affecting the availability
Condition-1: If the temperature of heat source does not remain same while supplying a given amount of heat, Qh to the system, then the available energy reduces as shown on T-S diagram in figure 8.4
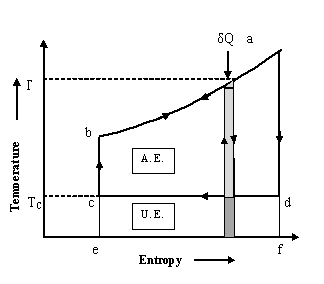
Fig. 8.6 Reduction in A.E. due to decrease in temperature of heat source
If, we apply a
number of reversible engines, each taking heat, δQ from
the source at constant temperature T but which is different for each engine and
vary between Ta to Tb for different engines. Then the A.E
can be determined by integrating δQ
TC.dS between the initial and final temperatures of heat
sources.
![]()
Where, m & C
are the mass and specific heat of matter working as heat source.
![]()
It will be clear by solving the numerical problem given below.
Total energy supplied by heat source, Q is shown by area a-b-e-f on T-S chart shown in fig 8.6.
Available Energy, A.E. is shown by area a-b-c-d on T-S chart shown in fig 8.6
Unavailable
Energy, U.E. is shown by area c-d-e-f on T-S chart shown in fig 8.6
Example: Estimate the A.E contained in 1 Kg of water at 1000C and 1 atm pressure with respect to surroundings at 300C.
Solution: Let the water be cooled from 1000C (373K) to 300C (303K) while supplying heat in a number of steps to reversible heat engines, operating in series and rejecting heat to surroundings at temperature 30°C. So temperature, T of heat source (water) is varying. And temperature, TC of surroundings (heat sink) is 30°C.
Then available
energy of a reversible heat engine absorbing heat δQ from heat source at temperature, T
and rejecting at Tc is given by
![]()
Therefore total
maximum work, which can be available from water cooled from 1000C to
300C will be
![]()
![]()
![]()
![]()
![]()
Thus in this case available energy is only about 10% of total energy.
Condition-2
In real conditions, heat is transferred from heat source to working substance only when there is some finite temperature difference between both. So, there is loss of available energy due to heat transfer through a finite temperature difference.
If there is no
temperature difference between heat reservoir and working substance of heat
engine and heat given by reservoir at temperature Th is Q when the
surrounding is at temperature, Tc
then,
![]()
But, if there is
finite temperature difference, such that working substance is at temperature ![]() lower
than Th of heat source then for the same heat Q given to heat
engine, the entropy change of working substance in heat engine will be more as
shown in Fig.
8.7.
lower
than Th of heat source then for the same heat Q given to heat
engine, the entropy change of working substance in heat engine will be more as
shown in Fig.
8.7.
As Q = Th ∆S = Th′ ∆S′
So if Th′ < Th then ∆S′ > ∆S
And the
available energy, A.E., in case the heat engine absorbs heat at temperature ![]() will
be
will
be
![]()
Loss in A.E
![]()
![]()
For the same
heat absorbed, ![]()
![]() (Shown
by shaded region in Fig.
8.7)
(Shown
by shaded region in Fig.
8.7)
Example: In a boiler for generating steam, water is evaporated at 200oC while the combustion gases are cooled from 1350oC to 350oC. The specific heat of gases at constant pressure is 1.1 kJ/ kg K. The surroundings are at 30oC. Determine the loss in A.E.
Solution: Had
the heat transfer from hot gases to water been reversible and water/steam would
have been heated from b to a and expanded from a to 3 as shown in fig
8.6 then the resulting U.E would have been as shown by area: ![]()
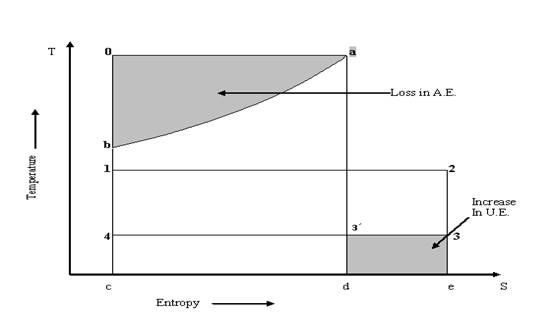
Fig. 8.8 Loss in A. E. and Increase in U. E.
But in actual the water is being heated at 2000C from 1 to 2.
So, Heat Rejected by hot gases (Area a-b-c-d) = Heat absorbed by water (Area 1-2-e-c)
Due to decrease in temperature of hot gases, there is direct loss in A.E shown by shaded area a-0-b.
Due to the
finite temperature difference between the gases and water, there will be loss
in A.E or gain in U.E shown by shaded area ![]()
To calculate this, we require finding the difference between entropy change of gases and water.
Entropy increase
for 1 kg of water
![]()
Where, hfg = Latent heat of water at saturation temperature of 200o C
By doing energy balance in boiler, mass of hot gases used per kg of water can be calculated as:
mg (1.1). (1350-350) = 1938.50
or mgas = 1.762 kg / kg of water
Entropy decrease
of gases
![]()
![]()
Difference in
entropy change of water and hot gases, ∆S
= 4.1
1.8557 = 2.244 kJ/kg K
![]()
= 303x 2.244 = 679.93 kJ / kg of water
So, due to
temperature difference, increase in Un-available Energy ![]()
= 303x 2.338
= 708.414 kJ/ kgK
(Ans)