Module 4. Second law of thermodynamics
Lesson 9
GENERAL EXPRESSION FOR CHANGE IN ENTROPY, NUMERICAL PROBLEMS
9.1 General Expression for Change in Entropy of a Perfect Gas during a Non Flow process
We know that first law of thermodynamics applied to a non-flow reversible process is:
δQ = dU + δW
Or δQ = mCv∆T + P.dV
Incremental
change in Entropy during a reversible process is given as:
![]()
![]()
![]()
![]()
Total change in entropy during process 1-2 will be

![]()
![]() (Eq. 9.1)
(Eq. 9.1)
By equation 9.1, we can calculate change in entropy in terms of change in temperature and change in volume during a non flow reversible process 1-2.
From the
perfect gas equation, we know that ![]()
Putting it in eq
9.1
![]()
![]()
![]()
![]() (Eq. 9.2)
(Eq. 9.2)
By equation 9.2,
we can calculate the change in entropy in terms of change in temperature and change
in pressure during a non flow reversible process 1-2
![]()
![]()
![]()
![]() (Eq. 9.3)
(Eq. 9.3)
With the help of equation 9.3, we can calculate change in Entropy in terms of change in pressure and change in volume during a non-flow reversible process 1-2.
9.1.1 Change of entropy during a polytropic process
We know that a
small heat exchange, δQ during a polytropic
process is given as
![]()
![]()
![]() (Eq. 9.4)
(Eq. 9.4)
This is the
expression for change in entropy in terms of change in volume only
We know that
during a polytropc process, ![]()
Putting this
value in eq 9.4
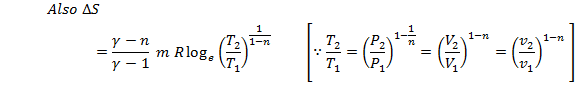
![]()
![]() ;
;
![]() (Eq. 9.5)
(Eq. 9.5)
This is the expression for change in entropy in terms of change in temperature only.
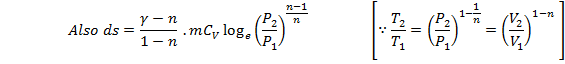
![]()
Putting these values
![]() (Eq. 9.6)
(Eq. 9.6)
This is the expression for change in entropy in terms of change in pressure only.
![]()
![]()
Putting these values
![]()
![]() (Eq. 9.7)
(Eq. 9.7)
9.2 Numerical Problems
9.2.1 A cyclic heat engine operates between a heat source temperature of 900o C and heat sink temperature of 30oC. Find the least rate of heat rejection per kW of net power output produced by the engine.
Solution
Given that
Absolute temperature of source
Th = 900 + 273 = 1173 K
Absolute temperature of heat sink,
Tc = 30 + 273 = 303 K
Now the least rate of heat rejection will only come in case of reversible heat engine, because it has the highest efficiency to convert heat from heat source into work.
Efficiency of reversible heat engine between the given source & sink temperatures is calculated as:
![]()
![]()
![]() Thus
heat absorbed from heat source for producing 1 kW of power
Thus
heat absorbed from heat source for producing 1 kW of power
![]()
Hence the least heat rejected will be equal to
Qc = Qh W
= 1.35 1
= 0.35 kW = 350 W (Ans)
9.2.2 Air at 15oC and 1.05 bar occupies 0.02 m3. The air is heated at constant volume until the pressure is 4.2 bar, and then cooled at constant pressure back to its original temperature. Calculate the net heat flow to or from the air and net entropy change.
Solution
The two processes are constant volume heating, and then constant pressure cooling to the same initial temperature 150C
Initial conditions of air are given as
Pressure, P1 = 1.05 x 105 Pa
Temperature T1 = 15+273 = 288 K
Volume, V1 = 0.02 m3
Conditions after constant volume heating are given as
P2 = 4.2 x 105 Pa
V2 = V1 = 0.02 m3
Final temperature,
T2 can be calculated
from gas law ![]()
![]()
= 1152 K
Then the air undergoes the constant pressure cooling process 2-3 and conditions after that will be
P3 = P2 = 4.2 x 105 Pa (Constant Pressure Process)
T3 = T1 = 288 K (Given)
V3
can be calculated from gas law![]()
![]()
![]()
Mass of air can be calculated by the given conditions at any state as.
![]()
= 0.0254 kg
Net Heat Exchanged by air
Heat absorbed during constant volume heating
= mCv (T2−T1)
= .0254 x 717 x (1152-288)
= 15735 J
Heat rejected during constant pressure cooling
= mCp (T2−T3)
= .0254 x 1005 x (1152-288)
= 22055 J
Net heat exchange = Heat Rejected Heat absorbed
= 22055 15735
= 6320 J
i.e. Net heat rejected by air = 6320 J (Ans)
Net Entropy Change of Air:-
Entropy change during Constant Volume process 1-2 is given as
![]()
Entropy change during constant pressure process 2-3 is given as
![]()
Net Entropy Change = S3 S1
![]()
![]()
= .0254 (-0.399) = -0.0101 kJ/K= (Ans)
Negative sign
means the entropy of air is decreasing.
9.2.3 Equal masses of a certain gas at same pressures but at different temperatures T1 and T2 (T1> T2) are mixed in a thermally insulated system. Find the net change in entropy of the Universe due to change in entropy of the system. Show that change is necessarily positive.
Solution
Let after mixing, the temperature of mixture is Tc
![]()
Now change in entropy of gas mass whose temperature has decreased from T1 to Tc
![]() [Sub Eq.
(i)]
[Sub Eq.
(i)]
Change in entropy of gas mass whose temperature has increased from T2 to Tc
![]() [Sub Eq. (ii)]
[Sub Eq. (ii)]
So Net Change in
Entropy of System
= ds1 +ds2
![]()
![]()
![]()
![]()
![]()
![]()
Also, we know
that A.M (Arithmetic mean) is always greater then G.M (Geometric mean). So
change is always +ve. Hence it is proved that change is necessarily positive.
9.2.4 0.2 kg of air at pressure = 1.5 bar and temperature = 300 K is compressed to a pressure of 15 bar according to the law PV1.25 = Constant, Determine:
(i) Initial and final parameters of air, (ii) Work done on or by air (iii) Heat flow to or from the air, (iv) Change of entropy
Solution
m= 0.2 kg; P1 = 1.5 x 105 Pa; T1= 300o K; P2 = 15x105 Pa; n =1.25
(i)
For
a polytrophic process with value of n = 1.25,
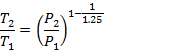
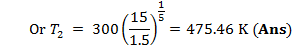
![]()
![]()
= 0.115 m3 (Ans)
Also
![]()
![]()
= 0.018 m3 Ans
(ii) Work exchange during a polytropic process is given as
![]()
![]()
= - 40285.6 J
= - 40.28 kJ (Ans)
Negative value of work exchange shows that work is done on the gas.
(iii) Heat Flow during polytropic process
![]()
= -15 kJ (Ans)
Negative value of heat exchange shows that heat is rejected by the gas
(iv) Change in Entropy for a polytropic process
![]()
![]()
= -39.9 ≈ - 40J/o K or -.04 kJ/o K (Decrease in Entropy)
(Ans)
9.3 Unsolved Problems
9.3.1 A Carnot cycle operates between source and sink temperatures of 2600 C and 17.8°C. If the system receives 100 kJ from the source, find (i) efficiency of the system, (ii) the net work transfer, (iii) heat rejected to the sink.
[Ans. 52.2%; 52.2 kJ; 47.8 kJ]
9.3.2 Source A can supply energy at a rate of 11,000 kJ/min at 3200C. A second source B can supply energy at a rate 110,000 kJ/min at 680C. Which source A or B, would you choose to supply energy to an ideal reversible engine that is to produce large amount of power if the temperature of the surroundings is 400C?
[Ans. Source B]
9.3.3 A heat engine is supplied with 278 kJ/s of heat at a constant fixed temperature of 2830C and the heat rejection takes place at 50C. The following results were reported: (i) 208 kJ/s are rejected, (ii) 139 kJ/s are rejected, (ii) 70 kJ/s are rejected.
Classify which of the results report a reversible cycle or irreversible cycle or impossible results.
[Ans. (i) Irreversible (ii) Reversible (iii) Impossible]
9.3.4 0.03m3 of nitrogen contained in a cylinder behind a piston is initially at 1.05 bar and 150C. The gas is compressed isothermally and reversibly until the pressure is 4.2 bar. Calculate the change of entropy, the heat flow, and the work done, and sketch the process on P-v and T-s diagrams. Assume nitrogen to act as a perfect gas. Molecular weight of nitrogen = 28.
[Ans. 0.01516 kJ/K (decrease) ; 4.37 kJ (heat rejected) ; 4.37 kJ]
9.3.5 0.05 kg of carbon dioxide (molecular weight = 44) is compressed from 1 bar and 150 C, until the pressure is 8.3 bar, and the volume is then 0.004 m3. Calculate the change of entropy. Take cp for carbon dioxide as 0.88 kJ/kg K, and assume carbon dioxide to be a perfect gas.
[Ans. 0.0113 kJ/K (decrease)]
9.3.6 A
rigid cylinder containing 0.006 m3 of nitrogen (molecular weight 28)
at 1.04 bar, 150C, is heated reversibly until the temperature is 900
C. Calculate the change of entropy and the heat supplied. Sketch the process on
T-s diagram. Take the isentropic index, γ, for
nitrogen as 1.4, and assume that nitrogen is a perfect gas.
[Ans. 0.00125 kJ/K; 0.407 kJ]
9.3.7 1 kg of air is allowed to expand reversibly in a cylinder behind a piston in such a way that the temperature remains constant at 2600 C while the volume is doubled. The piston is then moved in, and heat is rejected by the air reversibly at constant pressure until the volume is the same as it was initially. Calculate the net heat flow and the overall change of entropy. Sketch the processes on T-s diagram.
[Ans. -161.9 kJ/kg; -0.497 kJ/kg K]
9.3.8 A quantity of gas (mean molecular weight 36.2) is compressed according to the law pvn = constant, the initial pressure and volume being 1.03 bar and 0.98 m3 respectively. The temperature at the start of compression is 170C and at the end it is 1150C. The amount of heat rejected during compression is 3.78 kJ, cp = 0.92. Calculate :
(i)Value of n, (ii) Final pressure, (iii) Change in entropy.
[Ans.
(i) 1.33; (ii) 1.107 bar; (iii) 0.228 kJ/kg K]