Module 12. Boiler draught
Lesson 29
NATURAL DRAUGHT
29.1 Determination of the Height of Chimney for a Given Value of Natural Draught
For determination of the height of chimney required to produce certain amount of natural draught, we have to determine the density of flue gases inside the chimney, ρg and that of cold air outside the chimney ρa.
A shown in fig 29.1, if ‘H’ is the height of chimney and Pa is the atmospheric pressure at the top level of the chimney then

Fig. 29.1 Natural draught system
The absolute total pressure at grate level inside the chimney is given as
![]()
And total pressure at grate level outside the chimney
![]()
Then
draught produced, given by its definition will be equal to
![]() N/m2
(Pa)
.........
(Eq. 29.1)
N/m2
(Pa)
.........
(Eq. 29.1)
Where,
ρa
and ρg are in kg/m3
g = acceleration due to gravity = 9.81 m/sec2
H = Height of chimney in ‘m’
Calculation of ρa and
ρg
We know the combustion chemistry of carbon and hydrogen

From equation (i) & (ii) it is clear that volume of O2 supplied for combustion of a unit quantity of carbon is equal to volume of CO2 produced at same pressure and temperature and volume of O2 supplied for combustion of hydrogen is half of volume of steam produced at same temperature and pressure and volume of N2 supplied remains same at same temperature and pressure, as it does not take part in combustion.
Now, the hydrogen content in the fuel is very less because of which only, the volume of combustion product increases. So, it can be neglected and it is safely assumed that volume of products of combustion will be equal to volume of air supplied when both reduced to same temperature and pressure conditions.
Let m = mass of air required per kg of fuel burnt
Then mass of chimney gases = (m+1) kg per kg of fuel burnt
Let T = mean absolute temperature of chimney gases in K
T1= Absolute temperature of outside air in K
![]()
![]() .........
[Sub Eq. (i)]
.........
[Sub Eq. (i)]
Where, P is in N/m2, T in oK and Ra in J/kg K
And volume of (m+1) kg of flue gases
will also be same at temperature T1 i.e. ![]()
But hot flue gases are at
temperature T. So their volume at temperature T will be:
![]() (Considering
atmospheric Pressure Pa, Constant)
(Considering
atmospheric Pressure Pa, Constant)
![]()
![]()
![]() Density
of inside flue gases
Density
of inside flue gases
![]() .........
[Sub Eq. (ii)]
.........
[Sub Eq. (ii)]
Here pressure P is in N/m2, Ra in J/kg K and temperature in K
Putting
the value of density of fresh air at temperature T1 and of hot flue
gases at temperature T2 in equation 29.1
![]()
![]()
![]() .........
(Eq. 29.2)
.........
(Eq. 29.2)
Putting
the values of
Atmospheric
Pressure P = 101300 Pa (N/m2)
Ra
= Characteristic gas constant for air = 287 J/ kg K
and
g = Acceleration due to
gravity = 9.81 m/sec2
Draught Produced
![]()
![]() .........
(Eq. 29.3)
.........
(Eq. 29.3)
By this formula the theoretical height of chimney required may be determined for producing a certain amount of natural draught, if we know the absolute temperature of flue gases inside the chimney and of air outside the chimney and mass flow rate of air per kg of fuel burnt.
Actual Draught produced by chimney is generally less than 12 mm of water.
From equation 29.2, it may be seen that the draught produced by the chimney becomes more effective with increase in height of chimney and temperature of flue gases.
29.2 Determination of Diameter of Chimney
Let us find out the draught produced in terms of height of flue gases i.e. h meters.
So,
it will be expressed as pd = ρg. g. h
And From Equation 29.2
![]()
![]()
![]()
Putting the values of ρg from sub eqn (ii)
![]()
![]()
Now
assuming that draught losses are Nil and all the draught contribute to
imparting velocity to flue gases, velocity of flue gases can be given by:
![]()
If we take into account the
frictional pressure losses in chimney and let it be hf,
then
![]() .........
(Eq. 29.4)
.........
(Eq. 29.4)
![]()
Where k is a constant the value of which is given as
k= 0.825 for brick chimney, 1.1 for steel chimney
Also, the mass of flue gases flowing through any section of chimney will be given by
![]()
Or
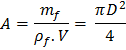
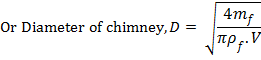
![]() .........
(Eq. 29.5)
.........
(Eq. 29.5)
In this way, the height and diameter of chimney to produce a given natural draught can be estimated theoretically.
29.3 Efficiency of Chimney
From equation 29.3, it is clear that for a given height of chimney draught depends on temperature of hot gases leaving the chimney. Natural Draught is directly proportional to outlet temperature of flue gases. It increases with the increase in outlet temperature. But high temperature of hot gases leaving chimney means the loss of heat energy and hence thermal efficiency of boiler. Thus natural draught is created at the cost of thermal efficiency.
However in artificial draught system, the flue gases can be made to leave the chimney at a reduced temperature, thus increasing the thermal efficiency or we can say that more heat of flue gases can be harnessed and given to steam. Thus the efficiency of chimney can be calculated on this basis:
Let T = Temperature of flue gases in natural draught
T2 = Temperature of flue gases in artificial draught
Cp = mean sp heat of flue gases in J/kg K
Then extra heat carried away by flue gases due to higher temperature required for producing natural draught = Cp (T – T2) for one kg of flue gases.
Draught Produced in terms of height
of column of exhaust
gases
![]()
It can give
maximum energy to one kg of flue gases = m. g. h ![]()
Thus efficiency of chimney can be
calculated as
![]() .........
(Eq. 29.6)
.........
(Eq. 29.6)
It is to be noted that even for a very tall chimney, the efficiency, will be
less than 1%. So it is a very inefficient mean to create draught. Due to this
reason for and for demand of energy efficiency, natural drought is not used in
most of the commercial boilers.