Module 12. Boiler draught

Lesson 30

POWER REQUIREMENT OF MECHANICAL DRAUGHT, NUMERICAL PROBLEMS

30.1  Power Required to Drive Fan in case of Mechanical Draught

We have come to know that, natural draught is produced at the cost of wasting a sufficient part of heat of flue gases through chimney. Moreover, maximum 1% of this energy can be used to produce natural draught and rest goes waste. On the other hand, in case of mechanical draught this waste going heat energy can be reduced significantly by using external energy of fans or blowers run by an electric motor. Heat energy of flue gases can be used within the boiler to a maximum level by using mechanical draught in place of natural draught. The energy or power required to drive a fan producing artificial draught can be calculated as:

Let, p_d = draught required to be produced in Pa (N/m²)

h_w = equivalent height of water column in mm. Such that p_d = (ρ_w × g × h_w) ÷ 1000

V = volumetric flow rate of air or flue gases in m³/sec

η_f = Efficiency of energy conversion of fan (Mechanical efficiency of fan)

Power imparted to air or flue gases by fan

......... (Eq. 30.1)

Actual power required by fan will be more than this and is given as

Putting the value of ρ_w = 1000 kg/m³ and g = 9.81 m /sec²

......... (Eq. 30.2)

Here V = volume flow rate of air or flue gases in m³/sec depending on the fan is blowing fresh air or flue gases.

30.1.1  In case of forced draught

Fan is handling fresh air from boiler room at normal room temperature. So its volume can be calculated from gas equation i.e.

Where m = mass flow rate of fresh air supplied

            T = Normal Room temperature

R_a = Characteristic gas constant

Using this volume in eq 30.2, power of forced draught fan can be calculated.

30.1.2  In case of induced draught

Already we have assumed that volume of fresh air supplied is same as volume of flue gases produced, if both are reduced to same temperature and pressure. Also, in the boiler, as draught is less so pressure of both fresh air and hot flue gases may be assumed same for the purpose of calculation of volume of gas. But the difference in temperature is significant which mainly cause the increase in volume of hot flue gases. Thus the volume of hot flue gases can be calculated as

So power required by induced draught fan can be calculated by plotting the value of V_g in place of V in equation 30.1

Naturally as T_g > T so  V_g > V

Power of Induced Draught fan > Power of forced draught fan

Thus power of induced draught fan is more than the power of forced draught fan in the same ratio as the temperature of flue gases is more than the temperature of fresh air, if all other factors mainly the efficiencies of fans are same.

30.2  Numerical Problems

30.2.1 With a chimney of height 45 meters, the temperature of outgoing flue gases with natural draught was 370^oC. The same draught was developed by induced draught fan and the temperature of flue gases was 150℃. Mass of flue gases formed is 25 kg per kg of coal fired. The boiler house temperature is 35^oC. Assuming C_p = 1.004 kJ/kg K for the flue gases. Determine the efficiency of chimney.

Solution

Height of chimney, H = 45 m

        Absolute Temperature of flue gases with natural draught, T = 370+273

                                               = 643^oK

Absolute Temperature of flue gases with artificial draught T₂ = 150+273

   = 423^oK

       Outside air’s absolute temperature, T₁ = 35+273 = 308 K

       Mass of flue gases formed, m+1 = 25 kg

       Mass of air supplied, m = 24 kg

       Sp heat of flue gases, C_p = 1004 J/kg K

      Now efficiency of chimney is given as:

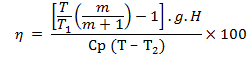
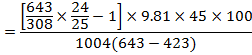
        = 0.2%   (Ans)

30.2.2 Determine the height and diameter of the chimney used to produce a draught for a boiler which has an average coal consumption of 1800 kg/hour and flue gases formed per kg of coal fired are 14 kg. Total pressure losses through the system are given as 20 mm of water.

Pressure head equivalent to velocity of flue gases passing through the chimney = 1.3 mm of water.

The temperature of ambient air and flue gases are 35^oC and 310^oC respectively. Assume actual draught is 80% of the theoretical.

Solution

Average coal assumption = 1800 kg/hour

mass of flue gases formed per kg of coal, (m+1) = 14kg

mass of air supplied per kg of coal, m = 13kg

Total pressure losses through the system, h_f = 20 mm of water

Pressure head equivalent to velocity of flue gases = 1.3 mm

 Actual Draught required (p_d)_ac = 20+1.3 = 21.3 mm

Temperature of ambient air, T₁ = 273 + 35 = 308 K

Temperature of flue gases, T = 310 + 273 = 583 K

Now Draught required theoretically in N/m²

= 261.2 N/m²

and which is given as

= 261.2 N/ m²

= 261.2

Or     4.846 H = 261.2

Diameter of Chimney

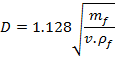
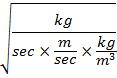
Now m_{f =} mass flow rate of flue gas in kg/sec

= 0.65 kg/ m³

Now velocity head of flue gases, h = 1.3 mm of water

= 2 m of flue gases

= 6.26 m/sec

Putting all the values, diameter of chimney

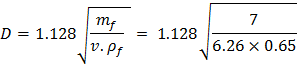
= 1.479 m            (Ans)

30.2.3 A chimney of height 32 m is used for producing a draught of 16 mm of water. The temperature of ambient air and flue gases are 27^oC and 300^oC respectively. The coal burnt in the combustion chamber contains 81% carbon, 5% moisture and remaining ash. Neglecting losses and assuming the value of burnt gases equivalent to volume of air supplied and complete combustion of fuel, find the percentage of excers air supplied.

Solution

Draught produced, p_d = 16 mm of water                                 

= 156.96 N/m²

Height of chimney, H = 32 m

Temperature of ambient air, T₁ = 273 +27 = 300 K

Temperature of flue gases, T = 300 +273 = 573 K

Now Natural Draught produced in chimney is given as

Or

 Or

Or

m+1 = 1.098 m

Or

 Mass of air supplied per kg of coal, m = 10.2 kg

Fuel analysis

Element Weight (kg)                                                      

C= 0.81 kg   

Amount of O₂ in kg

Total Amount of air for complete combustion

Actual Amount supplied = 10.2 kg

30.2.4 Calculate the power of motor needed to drive a fan for maintaining an artificial draught of 60 mm of water if the fan is working as a

a) Forced Draught Fan

Also if it is working as an

b) Induced Draught Fan

Use the following data of boiler:

Temperature of flue gases leaving the boiler = 250 ^oC

Temperature of boiler house = 20 ^oC 

Air supplied per kg of fuel = 19 kg

Mass of coal burnt per hour = 1800 kg

Efficiency of fan = 85%

Solution

Given that

Absolute temperature of flue gases, T_g = 250 + 273 = 523 K

Absolute temperature of air, T_a = 20 + 273 = 293 K

Mass of air used, m_a = 19 Kg/Kg of fuel

Mass of fuel used, M = 1800 Kg/hour

Value of artificial draught, h_w = 60 mm of water

Efficiency of fan, η_f = 85% = 0.85

Case I:  Power of forced draught fan

We know that the power of fan is given by

Where h_w = Draught in terms of mm of water

V_a = Volume of air supplied in m³/sec

Volume can be calculated from gas equation as

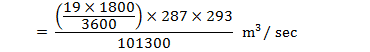
= 5461 W

Or        = 5.46 KW (Ans.)

Case II:  Power of induced draught fan

If the fan is used as Induced draught fan, than it has to handle volume of hot flue gases, which will be more than fresh air.

Volume of flue gases produced can be calculated as