Module 13. Air compressor
Lesson 32
AIR COMPRESSOR’S WORK, NUMERICAL PROBLEMS
32.1 Volumetric Efficiency in terms of Clearance Ratio ‘K’
Refer to the diagram 32.1. It is clear that after expansion, the clearance volume gas takes the volume V4 at which suction valve opens. So, the fresh air is sucked only from volume V4 to V1.
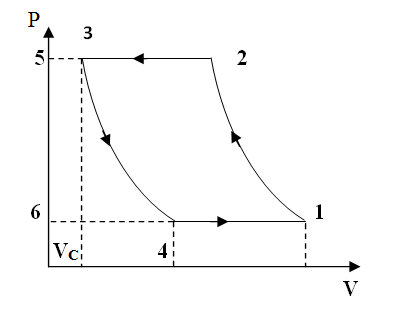
Fig. 32.1 P-V Diagram of single stage reciprocating air-compressor
So effective volume sucked of fresh air = V1 - V4
The pressure and temperature of this volume are P1 and T1.
If this air is reduced to intake or outside atmospheric pressure and temperature Pa and Ta, the actual volume of air sucked will be
![]()
![]()
As per the definition of volumetric efficiency:
![]()
![]()
![]()
![]() .........
(Eq. 32.1)
.........
(Eq. 32.1)
Consider the polytrophic expansion process 3-4
![]()
or
P2VnC = P1V4n
![]()
Substituting
this value in equation (1)
![]() .........
(Eq. 32.2)
.........
(Eq. 32.2)
If the ambient and suction conditions are same (i.e., considering only the effect of Clearance Ratio)
P1 = Pa and Ta
= T1
![]() .........
(Eq. 32.3)
.........
(Eq. 32.3)
This is the equation for volumetric efficiency in terms of Clearance Ratio.
32.2 Work Equation for Single Stage Compressor (Neglecting clearance Volume)
The theoretical cycle for single stage compressor without clearance volume is shown on P-V diagram as:
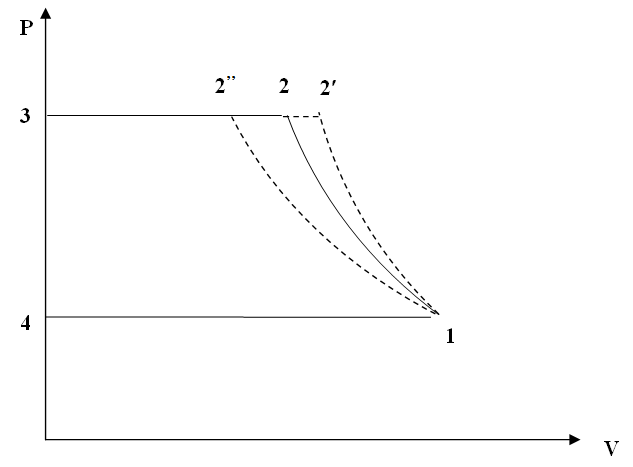
![]() :
Polytropic Compression
:
Polytropic Compression
![]() Adiabatic Compression
Adiabatic Compression
![]() :
Isothermal Compression
:
Isothermal Compression
Fig. 32.2 Compression cycle 1-2-3-4
Consider the polytropic compression ‘1-2’
Work done per cycle is area 1-2-3-4-1
W = Area under curve 1-2 + Area under curve 2-3 – Area under curve 4-1.
![]()
![]()
![]()
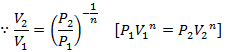
![]() .........
(Eq. 32.4)
.........
(Eq. 32.4)
32.3 Theoretical Work Considering Clearance Volume
The theoretical cycle of a single stage air-compressor with clearance volume is already shown in fig 32.1. From the diagram, it is clear that
Work done per cycle = Area under 1 2 3 4 1
Or W = Area 1-2-5-6-1 – Area 3-5-6-4-3
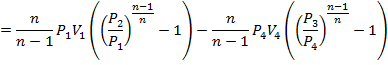
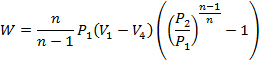
Now V1-V4 = Effective swept volume due to presence of clearance volume.
![]()
![]()
It usually varies between 60 to 85%
32.4 Multistage Compression with Inter Cooling

Fig 32.3 Multistage compression with zero value of C.V.
Neglecting clearance volume, the overall cycle diagram for multistage compression is as shown in fig 32.3
Work done in 2-stages of compression
= Work done in 1st stage
+ work done in 2nd stage
![]() .........
[Sub Eq. (i)]
.........
[Sub Eq. (i)]
We know P1V1= P3V3 for isothermal Process 1-3. Also for minimum work, pressure ratio per stage is equal i.e.,
![]()
Putting this in equation (1)
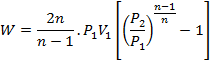
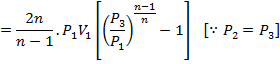

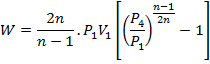
For
‘x’ number of stages of compression
![]() ......... (Eq.
32.5)
......... (Eq.
32.5)
When Pr= Total Pressure Ratio
32.5 Numerical Problems
32.5.1 A single stage reciprocating air compressor takes in 8m3/min of air at 1 bar and 300 C and delivers it at 6 bar. The clearance is 5% of the stroke. The expansion and compression are polytropic with the value of n=1.3. Calculate: (a) the temperature of delivered air; (b) volumetric efficiency, and (c) Power of the compressor.
Solution
Given that v1-v4 = 8 m3/min
p1 = 1 bar = 1x105N/m2
T1 = 300 C = 30+273 = 303 K
p2=6 bar = 6x105 N/m2
vc =5% vs = 0.05 vs
n= 1.3.
· Temperature of delivered air
Let T2= Temperature of the delivered air.
We know that for a polytropic compression process 1-2

![]()
· Volumetric efficiency
We know that clearance ratio,
![]()
![]() Volumetric
efficiency,
Volumetric
efficiency,
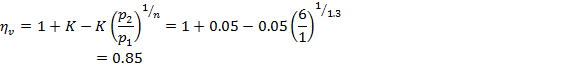
![]()
· Power of the compressor
We know that work done by the compressor,
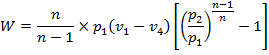

![]()
![]()
![]()
![]()
32.5.2. A single stage single acting reciprocating air compressor is required to handle 50 cum of free air delivery per hour measured at 1 bar pressure. The delivery pressure is 6.5 bar and the speed is 500 r.p.m.
Allowing a volumetric efficiency of 75%; an isothermal efficiency of 70% and a mechanical efficiency of 90%; Calculate the indicated mean effective pressure and the power required to drive the compressor.
Solution
Given: v1=50 m3/ hour
p1=1 bar = 1x105 N/m2
p2=6.5 bar = 6.5 x 105 N/m2
N = 500 r.p.m
ηv = 75% = 0.75
ηi = 70% =0.70
ηm = 90% = 0.9
1) Indicated mean effective pressure:
The expression for isothermal work done is given as
![]()
= 9359×103 J/h = 9359
kJ/hr
![]()
We know that swept volume of the piston,
![]()
![]()
![]()
= 200 kN/m2
= 2 bar (Ans.)
2) Power required in driving of the compressor:
Actual work done by the compressor is given as
![]()
![]()
32.5.3 A single stage double acting air compressor delivers 5 m3 of free air per minute at 1 ata and 200 C to 7.5 bar with the following data;
R.P.M. = 300; Mechanical efficiency = 0.9; Pressure loss in passing through intake valves = 0.04 bar; Temperature rise of air during suction stroke = 120 C ; Clearance volume = 5% of stroke volume; Index of compression and expansion, n=1.3; Length of the stroke = 1.3 times the cylinder diameter.
Calculate: 1. Power input to the shaft; 2. The volumetric efficiency; and 3. The cylinder diameter.
Solution
Given: Va= 5 m3/min
pa =1 ata= 1.013 bar
Ta= 200 C =20 +273 = 293 K
p2= 7.5 bar;
N = 300 r.p.m
ηm=0.9
Pressure loss = 0.04 bar
Temperature rise = 120 C
vc = 5%
vs =0.05 vs
n = 1.3
L = 1.3 D
Let V1=Volume of free air at the suction conditions.
As there is a pressure loss of 0.04 bar in passing through intake valves, therefore net suction pressure will be equal to
p1= pa-0.04 = 1.013-0.04 = 0.973 bar = 0.973 x 105 N/m2
Given that there is a temperature rise of 120 C of air during suction stroke, therefore temperature at the beginning of compression of air will be
T1 = Ta + 12 = 20 + 12 = 320 C = 32 + 273 = 305 K
By Ideal gas equation
![]()
![]()
1. Power input to the shaft
We know that indicated work done
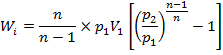
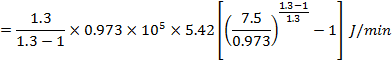
![]()
![]()
![]()
2. Volumetric efficiency
We know that clearance ratio,
![]()
![]()
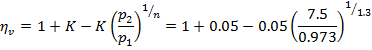
![]()
3. Cylinder diameter
Let D = Cylinder diameter, and
L = Stroke length = 1.3 D …………. (Given)
We know that swept volume per stroke
![]()
Since the compressor is double acting, therefore number of working strokes per minute = 2N =2x300=600 and swept volume per minute
![]()
We know that volumetric efficiency (ηv),
![]()
![]()
And
![]()