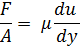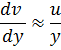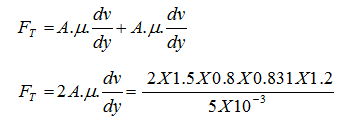Module 1. Introduction to fluid mechanics
Lesson 1
UNITS AND DIMENSIONS, PROPERTIES OF FLUIDS
1.1 Introduction
Fluid is a substance which has no definite shape and will continuously deform or flow whenever an external force is applied to it e.g. water, milk, steam, gas, etc. It cannot preserve its shape unless it is restricted into a particular form depending upon the shape of its surroundings.

Fig. 1.1 Fluids classified as liquids and gases
Fluid Mechanics is the study of fluids either in motion (fluid dynamics/kinematics) or at rest (fluid statics). Gases and liquids (e.g. air, water) come under the category of fluid.
One of the areas of modern fluid mechanics is Computational Fluid Mechanics which deals with numerical solutions using computers. Fluid mechanics comprises of the following subjects:

Fig. 1.2 Subjects covered under fluid mechanics
1.2 Why to Study Fluid Mechanics?
Fluid mechanics is one of the basic courses in Engineering. It is a bridge course between what you have already studied in physics and core B.Tech. courses which you will be studying after 1st year of your degree programme. Dairy plants handle various types of fluids such as milk, water, air, refrigerants, steam etc. It is very important to learn the behaviour of fluid under various conditions in order to design the system for handling of such fluids in dairy plants. Fluid mechanics is a branch of Engineering Science, the knowledge of which is needed in the design of:
- Water supply and treatment system
- Pumps used for handling of different fluids
- Ships, submarines, aeroplanes, Automobiles
- Storage tanks (milk silo, tankers, feed tanks,
balance tanks etc.)
- Piping systems for various utilities, pipefitting
& valves, flow meters etc.
- Measuring instrument
- Cleaning-In-Place (CIP) systems for optimum
performance
- Heat transfer behaviour in processing equipments
(such as HTST pasteurizers, spray dryers etc.)
1.3 Units and Dimensions
Solution to numerical and engineering problems becomes meaningless without units. One of the space projects of NASA, Mars pathfinder long back in 1999 crashed because the Jet Propulsion Laboratory engineers assumed that a measurement was in meters, but the supplying company’s engineers had actually made the measurement in feet (Fox et al., 2004). This incident truly represents the importance of units. A unit of measurement is a definite magnitude of a physical quantity. The different systems of unit are:
1. SI system: It is the International System of Units (abbreviated SI from the French Le Système International d'Unités.
2. CGS system: It is a system of physical units based on centimetre as the unit of length, gram as a unit of mass, and second as a unit of time.
3. MKS system: It is a metric system of physical units based on meter as the unit of length, kilogram as a unit of mass, and second as a unit of time.
4. FPS system The foot-pound-second system or FPS system is a system of units built on the three fundamental units foot for length, pound for either mass or force and second for time.
Table 1.1 Commonly used units in CGS, MKS, FPS and SI
|
Dimension |
CGS units |
MKS units |
FPS Unit |
SI units |
|
Length (L) |
Centimeter (cm) |
Meter (m) |
Foot (ft) |
meter, (m) |
|
Mass (M) |
Gram (g) |
Kilogram (kg) |
Pound (lbM) |
kilogram (kg) |
|
Time (T) |
Second (sec) |
Second (sec) |
Second (sec) |
Second (s) |
|
Force (F) |
Dyne (Dyn) |
Kilogram-force(kgf) |
Pound-force (lbF) |
Newton (N) (=kg m/s2) |
|
Temperature (θ) |
|
|
|
|
|
· Absolute |
Rankine (R) |
Celsius (°C) |
Kelvin (K) |
Kelvin (K) |
|
· Ordinary |
Fahrenheit (°F) |
Celsius (°C) |
Kelvin (K) |
Celsius (°C) |
Non-standard abbreviations:
fps = feet per second
gpm = gallons per minute
cfs or cusecs = cubic feet per second
cumecs = cubic meters per second
Note: Cusec and cumecs are non-standard abbreviations as it is widely used to measure large water flows.
· 1 British or imperial gallon = 1.2 U.S. Gallon (±0.1%)
· 1 U.S. gallon = 3.78 Litres
When not specified, assume U.S. gallons
Table 1.2 Unit prefixes in SI system
|
Factor |
Prefix |
Symbol |
|
109 |
Giga |
G |
|
106 |
Mega |
M |
|
103 |
kilo |
k |
|
10-2 |
centi |
c |
|
10-3 |
milli |
m |
|
10-6 |
micro |
μ |
|
10-9 |
nano |
n |
Table 1.3 Quantities, dimensions and units
|
Quantity |
Dimensions (M LT) |
Preferred units (SI) |
|
Length (L) |
L |
m |
|
Time (T) |
T |
s |
|
Mass (M) |
M |
kg |
|
Area (A) |
L2 |
m2 |
|
Volume (Vol) |
L3 |
m3 |
|
Velocity (V) |
LT-1 |
m/s |
|
Acceleration (a) |
LT-2 |
m/s2 |
|
Discharge (Q) |
L3 T-1 |
m3/s |
|
Force (F) |
MLT-2 |
N |
|
Pressure (p) |
ML-1T‑2 |
Pa |
|
Shear stress (τ) |
ML-1T‑2 |
N/m2 |
|
Density (ρ) |
ML-3 |
kg/m3 |
|
Specific weight (ω) |
ML-2T-2 |
N/m3 |
|
Energy/Work/Heat (E) |
ML2T-2 |
J |
|
Power (P) |
ML2T-3 |
W |
|
Dynamic viscosity (μ) |
ML-1T1 |
N s/m2 or Pa.s |
|
Kinematic viscosity (υ) |
L2 T-1 |
m2/s |
Some important units and conversions
Dyne = g cm/s2
1 dyne = 10-5 N
1 pound = 0.453 kg
Pressure: 1 atm = 101.325 kPa, 1 bar = 105 Pa
1 m = 3.28 ft
1 m = 100 cm
1 feet = 30.5 cm
1 feet = 12 inch
1 inch = 2.54 cm
1 km = 0.621 miles
1 ha = 2.47 acre
1 acre = 4 046.85 m2
1 litre = 0.264 gallon
°C = (5/9) × (°F – 32)
Table
1.4 Pressure conversion table
|
Pressure
units |
||||||
|
|
|
|
Technical
atmosphere |
|
|
Pound-force
per |
|
1
Pa |
≡
1 N/m2 |
10−5 |
1.0197×10−5 |
9.8692×10−6 |
7.5006×10−3 |
145.04×10−6 |
|
1
bar |
100,000 |
≡
106 dyn/cm2 |
1.0197 |
0.98692 |
750.06 |
14.5037744 |
|
1
at |
98,066.5 |
0.980665 |
≡
1 kgf/cm2 |
0.96784 |
735.56 |
14.223 |
|
1
atm |
101,325 |
1.01325 |
1.0332 |
≡
1 atm |
760 |
14.696 |
|
1
torr |
133.322 |
1.3332×10−3 |
1.3595×10−3 |
1.3158×10−3 |
≡
1 Torr; ≈ 1 mmHg |
19.337×10−3 |
|
1
psi |
6.894×103 |
68.948×10−3 |
70.307×10−3 |
68.046×10−3 |
51.715 |
≡
1 lbf/in2 |
Example
reading: 1 Pa = 1 N/m2 = 10−5 bar
= 10.197×10−6 at = 9.8692×10−6 atm = 7.5006×10−3 torr
= 145.04×10−6 psi
1.4
Properties of Fluid
1. Mass density (𝛒):
Mass of fluid per unit of its volume is called mass density.
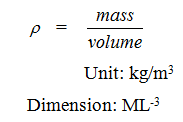
2. Weight Density (ω):
Weight of fluid per unit of its volume is called weight density.

3. Specific Gravity: Ratio
of density of a substance to the density of pure water at 4°C is called
specific gravity.

4. Specific Volume (v):
Volume of substance per unit of its mass is called specific volume.

Unit: m3/
kg
Dimension: M-1L3
5. Vapour Pressure
Liquid exhibits a tendency to vaporise or evaporate.
This process takes place at free surface of liquid where liquid molecules
continuously escape to atmosphere. The liquid molecules which escape from free
surface of liquid are in gaseous state, exert their own partial pressure on
surface of the liquid. This pressure produced by the molecules ejected is known
as the vapour pressure. Higher the vapour pressure of free liquid surface,
higher will be the rate at which molecules will escape into the
atmosphere.
·
Molecular activity increases with increase in
temperature resulting in increase in vapour pressure. Boiling occurs when
vapour pressure of the free liquid surface is equal to saturation vapour
pressure.
·
Saturation vapour pressure is attained when the space
above the liquid is saturated with vapours of the liquid. Equilibrium is
established between the liquid vapour interface in
which rate of molecules escaping from the liquid surface is equal to the rate
at which molecules return to the liquid. For a liquid saturation vapour
pressure is the maximum attainable vapour pressure at a given temperature.
Mercury has a very low vapour pressure (1.2 μmHg
at 20°C). Therefore, it is used in barometers and thermometers for accurate
results.
6. Cohesion:
It is intermolecular force of attraction between similar types of molecules.
7. Adhesion: It is the
force of attraction between molecules of:
a) Two different liquids which do not mix or
b) Between liquids and solid containing liquid.
8.
Compressibility:
i) Compressible
fluids: The fluids which undergoes a change in volume or density when pressure
is applied.
ii) Incompressible
fluids: The fluid which does not show a change in volume or density when
pressure is applied.
Compressibility is the property of the fluid due to
which there will be a change in volume when the fluid is subjected to an external
pressure and is reciprocal of Bulk Modulus of Elasticity (k).


9. Viscosity:
It is property of liquid which provides resistance to
flow. For example, flowability of honey is poor as compared to milk. Honey is
highly viscous. The viscosity of honey is much higher than milk.
1.5 Classification of Fluids
Types of
Fluids:
Ideal Fluid: Ideal
fluid is one which has no property other than density. Such fluids have no
viscosity, no surface tension and are incompressible. When such fluid flows, no
resistance is encountered. Ideal fluid is imaginary fluid as all the fluids
have some viscosity.
Real Fluid: The
fluids which have viscosity, surface tension in addition to density. All the
fluids have these properties whether large or small. The fluids can also be
classified in the following manner:
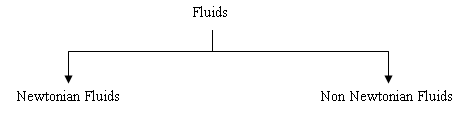
Fig.
1.3 Newtonian and non-Newtonian fluids
·
Newtonion Fluids: Fluids
which follow Newton’s Law of viscosity are called Newtonian fluid.
·
Non-Newtonion Fluids: Fluids
which do not obey Newton’s law of viscosity are called non-Newtonian fluids.
1.6 Newton’s Law of Viscosity
Consider
a fluid contained between two parallel plates as shown in the Fig. 1.4:
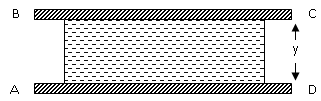

Fig.
1.5 Shear force is applied on the upper plate
Plate AD is the stationary plate where as BC is the
moving plate and distance between the plates is y units. Initially BC is at
rest. The area of the plate is A. Suppose a shear force is applied to top plate
at point B. By shear force we mean a force that is applied tangentially and
parallel to a surface. It can be seen in figure 1.5:
The upper
plate starts moving and attains a velocity say u m/s. Now the position changes
from ABCD to AB’C’D as shown in figure 1.6.
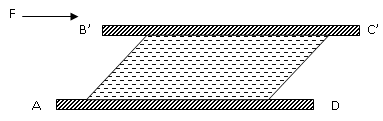
Fig.
1.6 Upper plate starts moving
As we
know, fluid molecules are arranged in layers. When the upper plate starts
moving, the fluid layer just touching the top plate starts moving the same
velocity. Then the next layer starts moving and so on. It can be seen in Fig. 1.7.
The distribution of fluid velocity from the top plate to the bottom is
known as velocity gradient or velocity profile and is given as:
![]()
Shear stress τ =
(shear force)/Area
τ is pronounced as Tau and is the symbol of shear
stress.
Note: shear stress is similar to pressure but here shear force is
involved
Here, shear stress is proportional to velocity gradient:
![]()
Or,
![]()
Here, μ is known as coefficient of viscosity or dynamic viscosity.
The SI unit of dynamic viscosity is Ns/m2.
CGS units of dynamic viscosity is
poise:
1 poise =
0.1 Ns/m2
1 Centi poise (CP) = 0.01 poise
Kinematic Viscosity:
![]()
SI
Units: m2/s
CGS
units = Stoke
1.7 Numerical
|
Q.1 |
A plate moves at 2 m/s with a shearing force of 3.5 N/m2. The distance between moving plate and fixed plate is 0.08 mm. Determine viscosity of fluid between plates. Solution: Velocity of plate (u) = 2 m/s
As dy is very small
= 1.4×10-2 Ns/m2 |
|
Q. 2 |
Two rectangular flat plates of dimensions 850 mm×600 mm are placed such that distance between plates is 20 mm. The space between them is filled with oil of specific gravity 0.92. The lower plate is fixed. The upper plate moves at 4.5 m/s and requires a force of 200 N to maintain this state. Determine dynamic and kinematic viscosity of oil. Solution: Velocity of plate (u) = 4.5 m/s Force (F) = 200 N Area of plate (A) = 850 mm × 600 mm Distance between plates (y) = 20 mm Density of subs = sp. gr × density of H2O at 4°C =0.92×1000 = 920 kg/m3
= 1.7429 Ns/m2
= 0.0018945 m2/s |
|
Q. 3 |
A liquid has specific gravity of oil is 1.85 and kinematic viscosity of 8 stokes. What is its dynamic viscosity? Solution: Kinematic viscosity = 8 stokes = 8×10-4 m2/s Density of substance = sp. gr × density of H2O at 4°C = 1.85×1000 = 1850 kg/m3 Dynamic viscosity = kinetic viscosity× density of subs
= 1.48 Ns/m2 |
|
Q. 4 |
The space between two parallel plates 5 mm apart is filled with crude oil. A force of 2 N is required to drag the upper plate at constant velocity of 0.8 m/s. The lower plate is stationary. The area of upper plate is 0.09 m2. Determine dynamic viscosity and kinematic viscosity if specific gravity of oil is 0.9. Solution: Distance between two plates (dy) = 5×10-3 Force required (F) = 2 N Area of plate (A) = 0.09 m2 Velocity of plate (v) = 0.08 m/s
= 1.38 Ns/m2 Specific gravity (sp. gr.) = 0.9
= 1.53 x 10-3 m2/s |
|
Q. 5 |
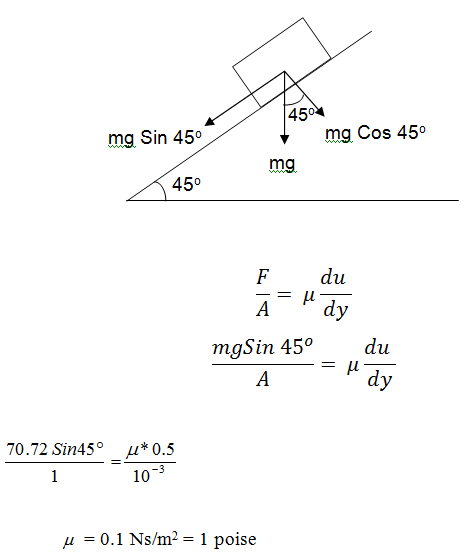
A plate has an area of 1m2, it slides down on inclined plane having angle of inclination 45° to the horizontal with a velocity of 0.5 m/s. The thickness of the oil filled between the plate and the plane is 1 mm. Find the viscosity of fluid if the weight of plate is 70.72 N. Solution: A = 1 m2, v = 0.5 m/s, y = 1 mm = 10-3 m, F = 70.72 N
|
|
Q. 6 |
The distance between two parallel plates is 10 mm, the space in between is filled with oil of viscosity 0.831 Ns/m2. A flat thin plate of dimensions 1.5 m × 0.8 m moves through the oil, calculate the force required to drag the thin plate at the velocity of 1.2 m/s when: a) Plate is moving at the centre b) The thin plate is at the distance of 3 mm from one of the plane surfaces. Solution: v = 1.2 m/s, A = 1.5 X 0.8 m2, µ = 0.831 Ns/m2
a) Ftotal = F1 + F2
= 478.656 N b) Ftotal = F1 + F2
= 398.88 + 170.95 = 569.83 N
|
Numerical Exercise
- A liquid has a specific gravity of 1.9 and
kinematic viscosity of 1 stoke. What is its dynamic viscosity? [Ans: 0.19 Ns/m2]
- The space between two parallel plates 5 mm apart
is filled with crude oil. A force of 1 N is required to drag the upper
plate at a constant velocity of 0.8 m/s. The lower plate is stationary.
The area of the upper plate is 0.09 m2. Determine: (i) The dynamic viscosity, and (ii) the kinematic
viscosity of the oil in stokes if the specific gravity of oil is 0.9. [Ans: 0.07
Ns/m2]
- A plate has an area of 1 m2. It slides
down an inclined plane, having angle of inclination 45° to the horizontal,
with a velocity of 0.5 m/s. The thickness of the oil film between the
plane and the plate is 1 mm. Find the viscosity of the fluid if the weight
of the plate is 71.72 N. [Ans: 0.000077 Ns/m2]
- A flat plate weighing 1 N has a surface area of
0.1 m2. It slides down an inclined plane at 30° to the
horizontal, at a constant speed of 3 m/s. If the inclined plane is
lubricated with an oil of viscosity 0.1 N.s/m2, find the
thickness of the oil film. [Ans: 0.101 m]
- A plate moves at 2 m/s with shearing force of 3.5
N/m2. The distance between the moving plate and fixed plate is
1 mm. Determine the viscosity of the fluid between the plates. [Ans: 0.060 Ns/m2]
- Two rectangular flat plates of dimensions 850mm X
600 mm are placed such that the distance between the parallel plates is 20
mm. The space in-between is filled with oil of specific gravity 0.92. The
lower plate is fixed. The upper plate moves at 4.5 m/s and requires a
force of 201 N to maintain this speed. Determine the dynamic and kinematic
viscosity of oil. [Ans: 0.002 Ns/m2,
2.17×10-6 m2/s]
- Determine the dynamic viscosity of a liquid
having specific gravity of 1.85 and kinematic viscosity of 8 stokes. [Ans: 1.752 Ns/m2]
- A flat thin plate is dragged at a constant
velocity of 1.2 m/s applying a force of 20 N. The lower plate is
stationary and the area of upper plate is 0.1 m2. Distance
between the plates is 10 mm. If the specific gravity of oil filled between
the plates is 0.92, calculate the dynamic and kinematic viscosity of oil. [Ans: 1.666 Ns/m2, 1.811 × 10-3 m2/s]
- Two large parallel flat plates are positioned 40
mm apart. A 2.5 mm thick plate of 0.5 m2 area is being towed in
lubricating oil filled between the plates with a constant force of 200 N.
Calculate the towing speed of plate when it remains equidistant from the
two parallel plates. The viscosity of the oil is 0.946 N.s/m2. [Ans: 3.9 m/s]
- The distance between two parallel planes is
10 mm. The space in between is filled with oil of viscosity 0.831 N.s/m2.
A flat thin plate of dimensions 1.5 m × 0.8 m moves through the oil.
Calculate the force required to drag the thin plate at a velocity of 1.2
m/s when:
a. the plate is moving at the center. [Ans: 478.65 N]
b. The
thin plate is at a distance of 3 mm from one of the plane surfaces. [Ans: 569.82 N]
- A steel shaft of 60 mm diameter slides
smoothly through a pipe of 65 mm internal diameter and length 120 mm. A
vertical force of 250 N is required to pull the shaft back to the original
position at the same constant speed. Determine the viscosity of oil filled
between the shaft and pipe. Take velocity as 4.5 m/s. [Ans: 5.67 Ns/m2]
- A cubical block weighing 20 kg and having a 20 cm
edge is allowed to slide down an inclined plane making an angle of 20°
with the horizontal on which there is a thin film of oil having viscosity
0.22 N.s/m2. What velocity will be attained by the block if the
film thickness is estimated to be 0.025 mm. [Ans:
0.19 m/s]
- A flat plate weighing 350 N is sliding on a
smooth inclined plate at 25° to the horizontal. The flat plate is moving
with a velocity of 1.35 m/s over the inclined surface. The inclined plate
is lubricated such that the thickness of lubricant applied between the
plane and plate is 2 mm. Determine the dynamic and kinematic viscosity of
fluid if the area of the moving plate is 0.8 m2. The density of
the lubricant is 1785 kg/m3. [Ans:
0.221 Ns/m2, 1.23×10-4 m2/s]
- In a stream of glycerin
in motion, at a certain point the velocity gradient is 0.25
s-1. The mass density of fluid is 1289 kg/m3
and kinematic viscosity is 5.2X10-3 m2/s. Calculate
the shear stress at the point. [Ans: 1.6757
N/m2]