Module 5. Fluid flow

Lesson 12

CONTINUITY EQUATION

12.1  Introduction

Continuity equation is one of the widely used formulae in Fluid Mechanics. The equation based on the conservation of mass is called continuity equation. When fluid flows in any pipeline, the rate of fluid flowing at every section remains constant.

12.2 Continuity Equation

It is based on principle of conservation of mass and is expressed by the following relation.

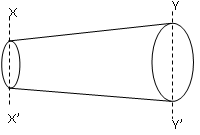
Consider a pipe of varying diameter as shown in (Fig 12.1). The fluid is compressible and the density at section XX’ is ρ₁ and at YY’ is ρ₂.

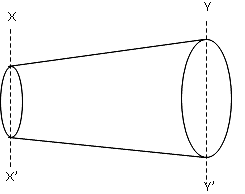
Fig. 12.1 Pipe of increasing diameter

At section XX’:

          Area of pipe = A₁

          Velocity of fluid = V₁

          Density of fluid = ρ₁

At YY’:

          Area = A₂

          Velocity=V₂

          Density = ρ₂

Volume flowing = A₁V₁ at section XX’

Mass of fluid flowing per second at section XX’ = ρ₁A₁V₁…………. (i)

Mass of flowing/sec at section YY’ = ρ₂A₂V₂ ……………..(ii)

Mass flow rate into the system = Mass flow rate out of the system

For compressible fluid applying conservation of mass,

ρ₁A₁V_{1 =} ρ₂A₂V₂   (Mass flow rate remains constant)

For incompressible fluid

ρ = constant i.e. ρ₁=ρ₂= ρ

∴ A₁V₁ = A₂V₂

Discharge, Q = AV 

At XX,  Discharge (m³/s) Q_{1 =} A₁V₁

At YY, Discharge (m³/s) Q_{2 =} A₂V₂

According to continuity equation,

Q₁ = Q₂

Thus, continuity equation relates flow velocity with area of the section, if area of flow at any section is decreased there is an increase in flow velocity.

12.3 Numericals

Q 1. The area of a pipe at section XX’ is 315 cm². The area of pipe at section YY’ is twice the area of section XX’. The velocity at section XX’ is 4.5 m/s. Find the velocity at section YY’. Also determine the flow rate through the pipe.

Solution:

A₁V₁ = A₂V₂

315 × 10^-4 × 4.5 = 630 × V × 10^-4

Discharge = A₁V₁

= 315 × 10^-4 × 4.5

                 = 1417.5 × 10^-4

                 = 0.14175 m³/s

Q 2. A compressible liquid is flowing in a pipe. The diameter of section XX’ and YY’ is 150 mm and 250 mm respectively. The density at XX’ is 998 kg/m³ and at YY’ is 994 kg/m³. If the velocity of liquid at section XX’ is 3.5 m/s, find the velocity at section YY’.

Solution:

ρ₁A₁V₁ = ρ₂A₂V₂

998 x π/4 × 150² × 10^-6 × 3.5 = 994 × π/4 × 250² × 10^-6 × V₂

Q 3. A pipe 500 mm in diameter bifurcates into two pipes of diameter 200 mm and 350 mm respectively. If the flow is incompressible and the velocity of flow in 500 mm and 200 mm pipe is 4.0 m/s and 3.0 m/s respectively. Find the (a) Discharge through 500 mm & 350 mm diameter pipe.

Solution:

Discharge through 500 mm = (π/4) × 500² × 10^-6 × 4 m³/s

Q₁ = Q₂ + Q₃

Or,

12.4 Numericals

Q.1. A incompressible liquid is flowing in a pipe. The diameter of section XX’ and YY’ is 170 mm and 200 mm respectively. If the velocity of liquid at section XX’ is 5.5 m/s, find the velocity at section YY’.

Q. 2. A compressible liquid is flowing in a pipe. The diameter of section XX’ and YY’ is 50 mm and 100 mm respectively. The density at XX’ is 995 kg/m³ and at YY’ is 990 kg/m³. If the velocity of liquid at section XX’ is 5.5 m/s, find the velocity at section YY’.