Module 7. Flow through orifices, mouthpieces, notches and weirs
Lesson 20
DISCHARGE LOSSES, TIME FOR EMPTYING A TANK
20.1 Discharge Losses
In an orifice actual discharge is always less than the theoretical discharge due to the following losses
a. Energy loss due to fluid viscosity
b. Formation of vena contracta, thus it reduces the area of flow.
Such losses are expressed using coefficient of discharge Cd. Coefficient of discharge for an orifice is the ratio of actual discharge to theoretical discharge.
![]()
20.2 Time for Emptying a Tank
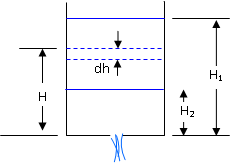
Fig. 20.1 Tank emptied from an orifice in the bottom
Area of orifice = a
Area of tank = A
Suppose the liquid level from H1 falls to H2 in time T seconds.
Suppose in time dt the fall in level is dh.
Volume of fluid discharged in time dt = (A dh) ......... (1)
Volume of fluid discharged from orifice = ![]()
Equating both equations
- (A dh) = ![]()
[-ve sign is from the fact that the head on the orifice decreases with increasing time]
![]()
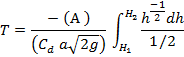
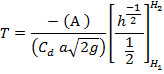
![]()
![]()
When tank is empty H2 = 0
![]()
Note: The above equation is also applicable in case where the orifice is at the side wall of the tank. Head is measured from the centre of the orifice to the free surface of the liquid.
20.3 Time of Emptying a Circular Horizontal Tank
Consider a circular horizontal tank filled with liquid and having an orifice at its bottom.
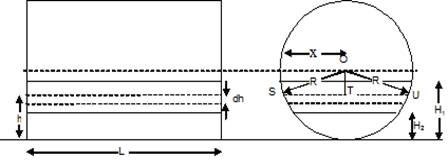
Fig. 20.2 Horizontal circular tank emptied from an orifice in the bottom
R = radius of the tank; L = length of the tank;
H1 = initial height of the liquid; H2 = final height of the liquid
a = area of orifice
T = time in seconds for the liquid to fall from height H1 to H2
Suppose at any instance height of the liquid in tank is h and there is decrease by dh distance in time dt. If x is the radius of liquid surface, at distance h from the orifice.
Volume of liquid leaving the tank in time dt.
=A
dh = SU × L × dh
![]()
=2x
L dh ……… (i)
Flow
velocity through the orifice = ![]()
Discharge
through orifice in time dt,
=
Cd × area of orifice × flow velocity × dt
= Cd a ![]() dt ………
(ii)
dt ………
(ii)
Since volume of liquid leaving the tank = volume of liquid
flowing through the orifice
Equating (i) & (ii)
![]()
Negative sign in above equation is because of decrease in
head on the orifice with increasing time.
![]() ………
(iii)
………
(iii)
From the geometry of horizontal circular tank,
OS = R and OT = (R-h)
![]()
Substituting this value of x in (iii)

Total time T to empty tank from height H1 to H2
can be calculated by integrating above expression between H1 and H2.
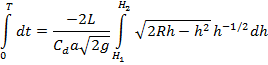
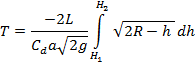
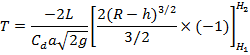
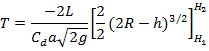
![]() ………
(iv)
………
(iv)
Case 1: Time for emptying the tank completely (H2 =
0)
From (iv)
![]()
Case 2: Tank is half-full at the beginning and is being
emptied
H1 = R and H2 = 0
From (iv)
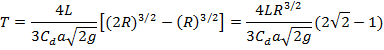
![]()