Module 7. Flow through orifices, mouthpieces, notches and weirs
Lesson 21
EXTERNAL AND INTERNAL MOUTHPIECE
21.1 Mouthpiece
Mouthpiece is an extended form of orifice in which a tube or pipe is attached to the orifice. The length of pipe attached to the orifice is 2 to 3 times diameter of orifice (Fig. 21.1). A mouthpiece is used to measure discharge.
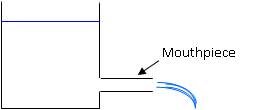
Fig. 21.1 Mouthpiece
21.2 Classification of Mouthpiece
Mouth piece can be classified as follows:
a. On basis of position
i. Internal: Pipe is fixed inside the tank/vessel
ii. External: Pipe is fixed and projected outside the tank walls
b. Flow pattern
i. Running free: Water jet after contraction in mouthpiece does not touches pipe internal walls.
ii. Running full: Water jet after contraction in mouthpiece touches pipe internal walls.
c. Shape of mouthpiece
According to the shape of the mouthpiece cylindrical, converging, converging-diverging etc
Table 21.1 Classification of mouthpiece on basis of position
* a = Area of mouthpiece
Table 21.2 Classification of mouthpiece on basis of shape

21.3 Flow Through an Internal Cylindrical Mouthpiece
Internal cylindrical mouthpiece is also known as Borda’s mouthpiece.
21.3.1 Borda’s mouthpiece running free
When the mouthpiece length is equal to its diameter, the liquid jet after contracting does not touch the sides of the tube. The mouth piece runs free i.e. without touching the tube.
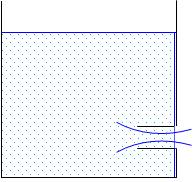
Fig. 21.2 Borda’s mouthpiece running free
Pressure force on mouthpiece = pressure × area of mouthpiece = ωH × α
Where,
ω = Weight density of liquid (ρg)
H = Height of liquid above the mouthpiece
α = Area of mouthpiece
αc = Area at vena contracta
V = flow velocity
Mass of liquid flowing per sec = ρ αc V
We know,
Momentum = mass X velocity
Rate of change of momentum = mass of liquid flowing/sec × change of velocity
= (ρ αc V) × (final velocity−initial velocity)
Placing,
Initial Velocity = 0
Final Velocity = V
![]()
![]()
Since weight density ω = ρg
![]() ………
(i)
………
(i)
![]() ………
(ii)
………
(ii)
Rate of change of momentum = Pressure force
Equating equation (i) and (ii)![]()
![]() ………
(iii)
………
(iii)
Torricelli’s equation ![]() ……… (iv)
……… (iv)
From equation (iii) and (iv)
![]()
Simplifying,
![]()
In case of no loss of head Cv = 1.0 ……… (v)
![]()
Since,
![]()
![]() ………
(vi)
………
(vi)
Cd = Cc × Cv ……… (vii)
From equ (v), (vi) and (vii)
Cd
= Cc × Cv = 0.5 × 1 = 0.5
![]()
Or,
![]()
21.3.2 Borda’s mouthpiece running full
Internal cylindrical mouthpiece is also known as Borda’s mouthpiece. Mouthpiece tube is about 3 times its diameter, the liquid jet after contraction in the tube touches the internal walls of the tube. Such a condition is known as mouthpiece running full (Fig. 21.3).
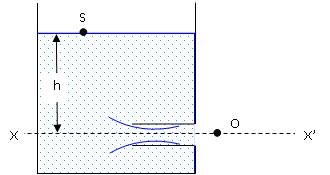
Fig. 21.3 Borda’s mouthpiece running full
Considering XX’ as datum line
|
|
At point S |
At point O |
|
Potential head or height from datum line |
h |
0 |
|
Pressure |
Ps |
Po |
|
Velocity |
Vs |
V |
Applying
Bernoulli’s theorem to the free liquid surface at point S and the outlet of
mouthpiece O,
![]() ………
(i)
………
(i)
Vs
= 0 as Vs << V and Vs is very small ……… (ii)
Pα = Po = atmospheric pressure ………
(iii)
![]() ………
(iv)
………
(iv)
Placing values of (ii), (iii) & (iv) in equation
(i)
![]()
![]() ………
(v)
………
(v)
From equation of continuity
Vc ac
= V a
![]()
![]()
Thus,
![]()
From equ v
![]()
Or,
![]()
Placing ![]() rom
Torricelli’s theorem in the above equation,
rom
Torricelli’s theorem in the above equation,
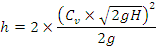
![]()
![]()
Coefficient
of contraction CC = 1
[Since
the area of jet at exit equals the area of the mouthpiece]
![]()
Discharge
through a Borda’s mouthpiece running full,
![]()
![]()