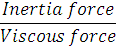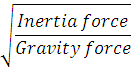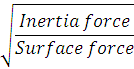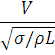Module 9. Dimensional analysis

Lesson 27

FROUDE  NUMBER,  REYNOLDS  NUMBER, WEBER  NUMBER

27.1 Dimensionless Numbers

In dimensional analysis, a dimensionless quantity is a quantity without an associated physical dimension. Dimensionless quantities are often defined as products or ratios of quantities that are not dimensionless, but whose dimensions cancel out when their powers are multiplied. This is the case, for instance, with the engineering strain, a measure of deformation. It is defined as change in length over initial length but, since these quantities both have dimensions L (length), the result is a dimensionless quantity.

27.2  Importance of Dimensionless Numbers

· The use of dimensionless numbers in engineering and physics allows the important task of data reduction of similar problems. This means that a lot of experimental runs are avoided if data is correlated using appropriate dimensionless parameters.

· Dimensionless numbers often correlate with some performance parameter and greatly aid engineering analysis and design.

· The value of the dimensionless numbers often reflects certain properties. For example, a flow problem with a low Reynolds Number will be laminar, while a larger value will imply turbulent behaviour.

· The number of dimensionless numbers determines the dimensionality of the space of solutions. For example, if a problem has two dimensionless numbers, then by varying both numbers, all the different behaviours in the problem can be accounted for.

· A dimensionless number can be used in the analysis of prototype models, to predict behaviour in similar full-scale systems. Dimensionless numbers help to compare two systems that are vastly different by combining the parameters of interest. For example, the Reynolds number, Re = velocity * length / kinematic viscosity. If an airfoil has to be tested with a particular Re, and simulation is conducted on a scaled-down model (length is smaller), one could increase fluid velocity or lower kinematic viscosity (change fluids) or both to establish the same Re and ensure working under comparable circumstances.

Table 27.1 List of few dimensionless numbers

Dimensionless No.	Significance	Group of Variables	Application
1. Reynolds Numbers			Laminar viscous flow in confined passage (pipes)
2. Froude’s Number			Free surface flow where effect of gravity is important.
3. Weber’s Number			Capillary & Sheet flow where surface tension is important.

27.3 Reynold Number (R_e)

In fluid mechanics, the Reynolds number Re is a dimensionless number that gives a measure of the ratio of inertial forces to viscous forces and consequently quantifies the relative importance of these two types of forces for given flow conditions.

Assume l represent a characteristic length in the flow system:

Inertia force F_i =  mass × acceleration

= density x Area x velocity x velocity

=

 [Since volume/time = Q = area × velocity]

=  

Thus

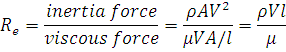
In the flow situations where the viscous forces plays an important, Reynolds number is taken as the criterion of dynamic similarity. Examples are as follows:

i. Incompressible flow through small diameter pipes,

ii. Objects moving completely under water,

iii. Air movement under low velocity around airplanes and automobiles

iv. Open channel flow.

27.4  Froude’s Number (F_r)

Froude’s number (Fr) is the ratio of the square root of the inertia force to the square root of the force due to gravity.

Gravity force = mass × gravitational acceleration

Froude number    

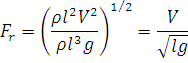
In flow situations where gravitational force is more important, Froude number governs the dynamic similarity. Other forces are comparatively small and negligible. Examples are:

i. Flow through open channels

ii. Flow of liquid jets from orifices

iii. Flow over notches and weirs

iv.  Flow over the spillway of a dam

27.5  Weber Number (W)

Weber number (W) is square root ratio of the inertia force to the force of surface tension.

Surface tension force = σ l

Where, σ is the surface tension per unit length.

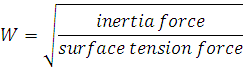
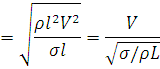
Application of Weber number:

i. Flow in Capillary tubes

ii. Thin sheet flow

iii. Liquid atomization