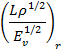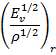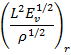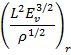Module 9. Dimensional analysis

Lesson 28

HYDRAULIC SIMILITUDE

28.1  Prototype and Model

Prototype

Prototype is the physical structure for which engineering design is required. The predictions are made for the prototype to work under actual field conditions.

Model

Model is the scale down representation of any physical structure. A model is smaller than the prototype so as to conduct laboratory studies and it is less expensive to construct and operate. Sometimes size of model can be larger than the prototype if amplified and more focused studies have to be carried out.

28.2  Importance of Model Studies

· Many of the equipments and hydraulic structures like dams, canals etc require lot of investment and time for construction.  A scale down model is tested under simulated condition to determine its performance. It saves time and resources. If the model fails it does not put financial pressure on the investors. Model can be easily improved and re-designing can be done if required.

· In many fields, there is great uncertainty as to whether a new design will actually do what is desired. New designs often have unexpected problems. A model is often used as part of the product design process to allow engineers and designers the ability to explore design alternatives, test theories and confirm performance prior to starting production of a new product

· Sometimes mathematical relationships and equations are not sufficient to aid in engineering design. A model provides valuable data on geometrical appearance, force and pressure distribution, performance, capacity etc.

· Experiments are conducted on models and the problems can be rectified before actual design and commissioning is done.

· By using model studies, alternate plans and modifications can be tested within a relatively short time with all flow conditions that can be expected. Also, the design and operating engineers can observe conditions resulting with a particular arrangement and satisfy themselves as to the adequacy of the plan.

· The cost of model studies varies with area of study, characteristics of the streams, nature of the problem, and number of plans and alternate plans to be tested before an acceptable solution is developed. The cost of model studies has usually been less than 0.10 percent of the cost of the project, a small price to pay for the assurance that the most practical and economical design has been developed.

28.3  Examples of Model Studies

· Models for builds are made to determine geometric appearance, stability under different wind velocities and patterns.

· Equipment and its components are first tested by making models for its performance.

· Hydraulic structures like dams, canals, reservoirs, spill ways  etc require model testing before its design is finalized.

· Automobiles, planes, rockets require model testing in wind tunnels.

28.4   Similitude

“Similitude” in a general sense is the indication of a known relationship between a model and prototype i.e. model tests must yield data that can be scaled to obtain the similar parameters for the prototype.

The results obtained model experiments can be applied to the prototype only if a complete similarity exists between the model and prototype and for that the two systems must be (i) geometrically (ii) kinematically and (iii) dynamically similar.

28.4.1 Geometric similarity

A model and prototype are geometric similar if and only if all body dimensions in all three coordinates have the same linear-scale ratio. It requires that the model and the prototype be of the same shape and that all the linear dimensions of the model be related to corresponding dimensions of the prototype by a constant scale factor. Usually, one or more of these pi terms will involve ratios of important lengths, which are purely geometrical in nature.

Thus for geometric similarity,

 Where,

l_m, b_m, h_m, and d_m =  respective dimensions of the model

l_p, b_p, h_p and d_p = corresponding linear dimensions of the prototype.

L_r  = constant known as scale ratio or the scale factor.

Area scale ratio  

 Volume scale ratio

28.4.2 Kinematic similarity

The motions of two systems are kinematically similar if homogeneous particles lie at homogeneous points at homogeneous times. In a specific sense, the velocities at corresponding points are in the same direction and are related in magnitude by a constant scale factor. This also requires that streamline patterns must be related by a constant scale factor. The flows that are kinematically similar must be geometric similar because boundaries form the bounding streamlines. The factors like compressibility or cavitations must be taken care of to maintain the kinematic similarity. 

Let points 1 and 2 represent the homologous (corresponding) points in the model and prototype. The conditions of  kinematic similarity are as follows:

Geometric similarity is a must for kinematic similarity. Therefore,

T_r is the time scale ratio, 

28.4.3 Dynamic similarity

When two flows have force distributions such that identical types of forces are parallel and are related in magnitude by a constant scale factor at all corresponding points, then the flows are dynamic similar. For a model and prototype, the dynamic similarity exists, when both of them have same length-scale ratio, time-scale ratio and force-scale (or mass-scale ratio).

· For compressible flows, the model and prototype Reynolds number, Mach number and specific heat ratio are correspondingly equal.

· For incompressible flows,

With no free surface: model and prototype Reynolds number are equal.

With free surface: Reynolds number, Froude number, Weber number and  Cavitation numbers for model and prototype must match.

Table 28.1. Flow characteristics and similitude scale ratios (ratio of prototype quantity to model quantity).

Characteristic	Dimension	Scale ratios for laws of
		Reynolds	Froude	Mach
Geometric
Length	L
Area	L^2
Volume	L^3
Kinematic
Time	T
Velocity
Acceleration
Discharge
Dynamic
Mass	M
Force
Pressure
Impulse and Momentum
Energy and Work
Power