Module 1. Alternating and direct current: Fundamentals

Lesson 4

FUNDAMENTALS OF ALTERNATING CURRENT

4.1 Introduction

In an A.C. system; the voltage acting in the circuit changes polarity (+ve & -ve) at regular time interval and therefore the current also changes direction accordingly. A.C systems are more widely used than D.C. system due to following reasons:

1. For large scale power generation, transmission and distribution ac systems are used to reduce transmission losses. Transformers are used to step up or step down alternating voltage efficiently. Thus handling alternating current is easier than D.C. system.

2. A.C. motors known as induction motors are simple in construction and also are cheaper compared to d.c motor.

The switch gears like switches, circuit breaker etc for A.C. system is simpler than D.C. system.

4.2 Generation of Alternating Voltage and Currents

An alternating voltage may be generated by

a) Rotating a coil in a uniform magnetic field.

b) Rotating a magnetic field within a stationary coil.

(Fig. 4.1 :Rotating a coil in a uniform magnetic field)

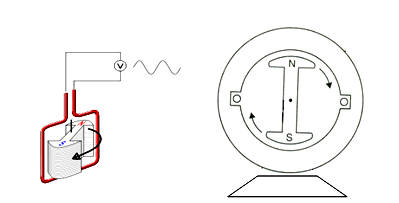
Fig. 4.2 Rotating a magnetic field within a stationary coil.

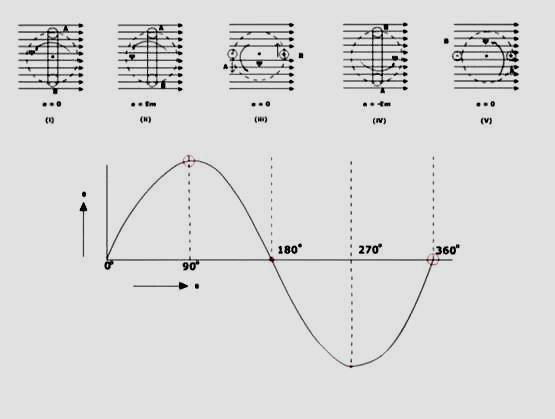
Fig. 4.3 Generation of A.C.

The alternating voltage generated by any of the above methods will be of sinusoidal waveform (i.e sine wave). The magnitude of generated voltage depends upon the speed of rotation, number of turns of coil and the strength of magnetic field. The equation for alternating voltage is given by:

e = E_m Sin ωt

Where,

e = Instantaneous voltage at any time t.

E_m = Maximum value of alternating voltage.

ω = Angular velocity of coil.

Alternating voltage in Sine waveform will produce sinusoidal current. There can be different types of alternating wave forms (Fig. 4.4).

Among different types of wave forms, sinusoidal wave is preferred over ramp, triangular or square wave because of following reasons:

· In A.C. system like induction motor and transformer, sinusoidal wave has lower losses with higher efficiency.

· Sinusoidal waves produce less noise or disturbance.

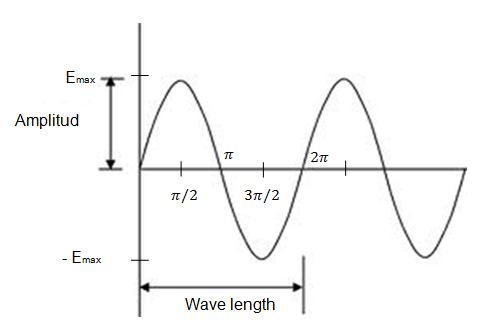
Fig. 4.5 A.C. sine wave

4.3 A.C. Terms

1. Wave form: Also known as wave shape is the shape of the curve obtained by plotting the instantaneous value of voltage or current in y-axis vs time in x-axis.

2. Cycle: an alternating quantity either voltage or current when completes one set of positive and negative values. One cycle is equal to 2π radian or 360⁰ electrical degree.

3. Alternation: One half cycle of alternating quantity either –ve or +ve half is called an alternation.

4. Instantaneous value: The value of an alternating quantity (voltage or current) at any instant is called instantaneous value.

5. Time period: The time required to complete one cycle of an alternating quantity is known as Time period. It is denoted by T and its unit is in second.

6. Frequency: The number of cycles per second of an alternating quantity is known as time period. Its unit is cycles/sec or Hertz (Hz). It is denoted by f.

Unit per second (1/s)

7. Amplitude: The maximum positive or negative value of alternating quantities is known as peak value or amplitude. It is denoted by E_max or I_max.

8. Angular velocity (ω): Angular velocity of rotating coil is given as:

Note: In one revolution the coil undergoes rotation of 2 π radiations.

4.4 Magnitude of Alternating Voltage and Current

There are three ways to measure magnitude of alternating voltage and current.

1. Peak value.

2. Average or mean value.

3. R.M.S value.

4.4.1 Peak value

The maximum value attained by an alternating quantity either voltage or current during one cycle is called the peak value. It is also known as amplitude and denoted as E_max or I_max.

4.4.2 Average value

The arithmetic mean of all the instantaneous values of an alternating quantity over one cycle is known as average value.

Since in symmetrical waves like sinusoidal current or voltage wave +ve half is equal to -ve half, the average value over a complete cycle is zero. Therefore, for alternating quantity average value is considered only for +ve half of the cycle.

4.5 Average Value of Sinusoidal Current

Consider an elementary area of width dθ in the +ve half of an alternating current. If i is the mid ordinate of the strip, then area of strip:

Area of strip = idθ

………(1)

Equating an alternating current

i = I_m Sin θ ………(2)

From equation (1) & (2):

I_ave= 0.637 I_max

Similarly for alternating voltage, average value of voltage is given as:

E_ave= 0.637 E_max

4.6 R.M.S Value (Root mean Square value)

The R.M.S value of an alternating current is the steady current or direct current which when flows through a known resistance for a given time produces the same amount of heat when the alternating current is flowing through the same resistance for the same time.

Consider the +ve half cycle of a non-sinusoidal alternating current I, flowing through a resistance R ohms for t seconds. Let divide the entire area into n equal parts as shown in the Fig. 4.6.

Let us consider that heat produced in the resistance R by current I is same as produced by direct current I flowing through resistance R for the same duration t seconds.

We know, heat produced in a resistance is given has:

Heat produced (q) = Current²×Resistance ×Time

q = i²Rt

………(1)

According to assumption heat produced by direct current I flowing through R for the same time is:

………(2)

As the heat produced in both the cases is same we can equate equation (1) and (2):

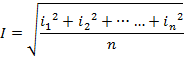
I = Square root of mean of squares of instantaneous values.

= Root-mean-square (r.m.s) value.

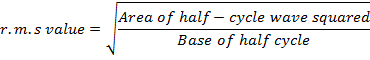
4.7 R.M.S Value of Sinusoidal Current

The equation for sinusoidal alternating current is given by:

i = I_max Sin θ ………(1)

The bold line in the figure shows sinusoidal current wave and the shaded line denotes i² value of the sinusoidal wave. (Fig. 4.7)

In the previous section we have already seen the formula for r.m.s value of current (I_rms):

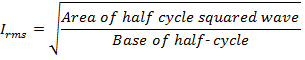………(2)

Consider an elementary area of width dθ in the +ve half cycle of the i² current wave.

Area of Strip = i² dθ

From equation (1):

Area of +ve half cycle of the squared wave:

………(3)

Base of half cycle = Π ……… (4)

Placing values from equation 3 and 4 in equation 2:

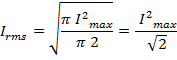
I_rms = 0.707 I_max

Similarly for sinusoidally alternating voltage r.m.s value can be given as:

E_r.m.s = 0.707 E_max

4.8 Form Factor

The ratio of r.m.s value to average value of an alternating quantity is known as form factor:

Form factor = 1.11

4.9 Peak Factor

Peak factor is the ratio of maximum value to r.m.s value of an alternating quantity is known as peak factor.

4.10 Numerical

Q.1. Calculate the frequency and angular velocity of an alternating quantity if the time period = 0.5 sec.

Sol.

Frequency f =

= 2 Hz or 2 cycles per sec

Angular velocity w = 2πf radians/sec

= 2π×2

= 22

= 12.14 radian/ sec.

Q.2 For an alternating quantity, I = 100 sin125t calculate

a. Maximum value of current

b. r.m.s value

c. Average value

d. Frequency

e. value of current after 0.005 sec.

Solution:

a. We know i = I_msinωt

I_m= 100A

b. I_rms= = = 70.70

c. I_ave= 0.637 I_m

= 0.637×100

= 63.7 A

d. sin ωt = sin125t

ω = 2πf

sin2πft = sin125t

2πft = 125

f = = 19.9

≅ 20 Hz

e. From the ques i = 100 sin 125t

i = 100sin125×0.005

i = 10.88 A

Q.3 For an alternating current i=75 sin 68t determine:

a. Maximum value

b. r.m.s value

c. Average value

d. Form factor

e. Frequency

Sol: a. we know for an alternating quantity.

i = I_maxsinωt

I_max= 75 A

b. I_rms=

= = 53.03A

c. I_ave= 0.637 I_max

= 0.637 × 75

= 47.77 A

d. form factor =

= 1.11

Q.4 Find the instantaneous value (equation) for alternating, voltage of 230v at 50 Hz for domestic supply.

Sol:

Equation for alternating voltage:

V = V_msinωt

V_m=230

= 325.26

ω = 2πf

= 2π50

= 314.15 radian/ sec

V = 325.26 sin 314.15t

Q.5 Calculate the term required by the current to obtain values of 25, 50 and 75 A. for a sinusoidal alternation current having maximum value of 150 A and frequency 50 Hz.

Sol: we know

i = I_max sinωt

I_max= 150A

a. Time for attaining 25 A

25 m = 150 sin (2π50t)

Sin2π50t =