Module 2. Static pressure of liquid

Lesson 3

PRESSURE HEAD OF A LIQUID, PRESSURE ON VERTICAL RECTANGULAR SURFACE

3.1  Pressure Force Acting on a Vertical Rectangular Surface

When the fluid is in static condition, there will not be any relative motion between adjacent fluid layers. The velocity gradient as well as shear stress will be zero. The forces acting on fluid particles will be due to pressure of fluid normal to the surface and due to gravity.

Consider a plane surface of arbitrary shape immersed vertically in a static mass of fluid as shown in Fig. 3.1.

Let,

C = Centre of gravity

P= Centre of pressure

= depth of centre of gravity from free liquid surface 1-1’

= depth of centre of pressure from free surface of liquid 1-1’

Fig. 3.1 A plane surface of arbitrary shape immersed vertically in a static fluid

The distance of centre of gravity from free surface is . Let P be the centre of pressure at which the resultant pressure on the rectangular plate acts.

Consider an elementary strip of ‘dx’ thickness and width b at the distance x from the free surface of liquid. Let pressure acting on the strip is p. If density of the liquid is ρ, then

Then total pressure force (F) acting on the elementary strip = p b dx

=  ρg 𝓍 b d𝓍

Total pressure force acting on whole area = ρg

Since = moment of surface area about the free liquid surface, we can take its value surface as .A

Then total pressure force, F = ρg .A.

(where ‘A’ is area of plate)

At point C pressure = ρg 

Total pressure force is equal to total area multiplied by the pressure at the centre of gravity of the plate surface immersed in the liquid.

3.2  Location of Centre of Pressure

The pressure on the immersed surface increases with depth. As shown in the following figure the pressure will be minimum at the top and maximum at the bottom of immersed plane.

Fig. 3.2 Location of centre of pressure

Suppose centre of pressure (P) is  from the free surface of the liquid;

Thus the resultant pressure will act at a point P much below the centre of gravity. Point P is known as the “centre of pressure” at which the resultant pressure acts on the immersed surface.

Total pressure force acting on the elementary strip = p b d𝓍

                                                                                          = ρg 𝓍 b d𝓍

Moment of pressure force about free liquid surface = ρg 𝓍2 b d𝓍

         Total moment of pressure force for entire area = ρg 

Since  = moment of inertia of entire surface about free surface 1-1’ = Io

Total moment of pressure force for entire area = ρgIo                                                                                                                                                                            ……… (i)

The sum of moment of pressure force = F                                                                                                                                                                                          ……… (ii)

Equating equation (i) & (ii):

F  = ρgIo

ρgA     = ρgIo

                                                                                                                                                                                                                                              ……… (iii)

From theorem of parallel axis for moment of inertia we have,

                                                                                                                                                                                                                                        ……… (iv)

Here,

 Ic = moment of inertia of area about an axis passing through centre of gravity.

 = distance of centre of gravity from free liquid surface

Placing value of Io into (iii),

Where, Ic is moment of inertia of the immersed figure;

 For rectangular surface Ic =       (b= base of rectangle, d= height or depth)

3.3  Numerical

Q1. A rectangular plate 4 m * 6 m is vertically immersed in water such that 6 m side is parallel to free surface. Calculate, the total pressure force and centre of pressure if the top of rectangular plate is: a) touching the free liquid surface, b) 3 m below the surface of water.

Solution.

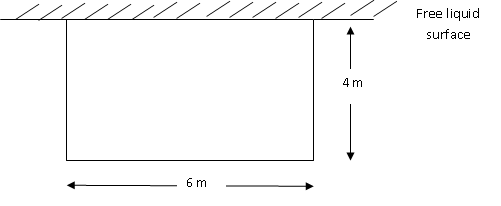
    a)  = 2 m; Area = 24 m2; ρ = 1000 kg/m3; g = 9.81 m/s

          Total pressure force       = ρg .A

                                      = 1000 ื 9.81 ื 2 ื 24

                                      = 470880 N

                                      = 470.88 kN

           

           

           

          Therefore,              = 2.67 m

    b) = 5m; Area = 24 m2; ρ = 1000 kg/m3; g = 9.81 m/s2

         

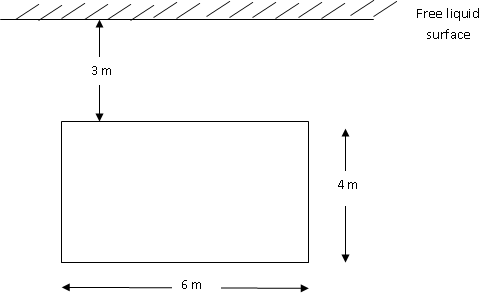
     Total pressure force = ρg .A

                                          = 1000 X 9.81 X 5 X 24

                                          = 1177200N

                                          = 1.1772MN

           

           

= 5.26 m

Q2. A rectangular plate 2 m ื 3 m is placed vertically in oil bath such that 3 m side is parallel to the free surface of liquid. Calculate the hydrostatic force and centre of pressure if the top of rectangular plate is 2.5 m below the oil surface. Specific gravity of oil = 0.1

Solution.

             = 3.5 m; A = 6m2; g = 9.8 m/s2

          ρ = 0.1 ื 1000 = 100 kg/m3

          Total hydrostatic force,

                   F = ρgA 

                      = 100 ื 9.8 ื 6 ื 3.5

                      = 20580 N   = 20.5 kN

           

  

          Put the value of Ic, A and  in relation of                  

 =

= 3.59 m