Module 3. Dimensional analysis and heat transfer
Lesson 12
CONDITIONS OF HYDROMECHANICAL SIMILARITY: DIMENSIONLESS NUMBERS
12.1 Conditions of Hydro-mechanical Similarity
Hydro-mechanical similarity determines the conditions in which similar flows occur in geometrically similar systems. Let us examine these conditions for the incompressible fluid flow.
Equation of continuity
![]()
Equation of flow
![]()
And for the second system, respectively
![]()
![]()
As the considered processes are similar, from the definition of similarity we have
![]()
![]()
These relationships are used to express all the variables of the second system by the variables of the first system in the following manner:
![]()
![]()
Substituting the values in equation of second system
![]()
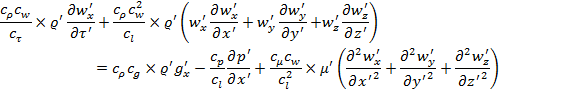
Both systems are now expressed by the variables of the first system. These variables from both systems must be determined in a similar manner. The latter stipulation is possible only if the equations are identical, and they require the dimensionless groups made up of the similarity constant to be cancelled from the system.
From the continuity equation it follows
that ![]()
This relationship does not limit the
choice of similarity constant. Because the equation remain identical for any
values of the ratio ![]() .
.
From the equation of flow
![]()
Investigating the members in pairs, we have
![]()
![]()
![]()
![]()
Such re-arrangement gives
![]()
![]()
![]()
![]()
Where
Ho = the homochronocity number
Fr = the Froude number
Eu = the Euler number
Re = the Reynolds number
The hydro-mechanical similarity of two or several systems, therefore, requires the numerical values of the Ho, Fr, Eu and Re numbers to be equal at any corresponding points of the systems.
In practical consideration these dimensionless numbers are modified with a view to give them a more convenient form easy to understand and interpret. So we have,
![]()
Where Ga = Gallilian number
![]()
Where Ar = Archimedes
Number
ρ, ρ0= fluid density at two different point of system.
If difference in density depend upon temperature difference then,
![]()
β = Fluid Expansion Factor
Substituting these values, we get
![]()
Where Gr = Grashoff Number
It should be clearly understood that all these dimensionless terms Fr, Ga, Ar, Gr are identical because these numbers are four different forms of one and same criteria.
Similarly Euler Number is also modified. The pressure term in Euler Number is replaced by difference in pressure at any two points in system.
![]()
The drop in pressure in pipe is most often sought for value in engineering study in which fluid is flowing. Therefore, the interdependence of dimensionless groups which may characterize a particular flow (say forced flow), then Eu = f [Re]. This functional relationship holds for all similar steady-state processes but function itself is to be determined experimentally.