Module I. Introduction to computer programming
Lesson 2
PROBLEM SOLVING WITH COMPUTER PROGRAMMING –
PART II
(Pseudo Codes and Analysis of Algorithms)
2.1 Pseudo Code
Pseudo code is a shorthand notation for programming, which uses a combination of informal programming structures and verbal descriptions of code. Emphasis is placed on expressing the behaviour or outcome of each portion of code rather than on strictly correct syntax.
In general, pseudo code is used to outline a programme before translating it into proper syntax. This helps in the initial planning of a programme, by creating the logical framework and sequence of the code. An additional benefit is that because pseudo code does not need to use a specific syntax, it can be translated into different programming languages and is, therefore, universal. It captures the logic and flow of a solution without the bulk of strict syntax rules.
It uses the structural conventions of a programming language, but is intended for human reading rather than machine reading. Pseudo code typically omits details that are not essential for human understanding of the algorithm, such as variable declarations, system-specific code and some subroutines. The programming language is augmented with natural language description details, where convenient, or with compact mathematical notation. The purpose of using pseudo code is that it is easier for people to understand than conventional programming language code, and that it is an efficient and environment-independent description of the key principles of an algorithm. It is commonly used in textbooks and scientific publications that are documenting various algorithms, and also in planning of computer programme development, for sketching out the structure of the programme before the actual coding takes place.
No standard for pseudo code syntax exists, as a programme in pseudo code is not an executable programme. Pseudo code resembles, but should not be confused with, skeleton programmes including dummy code, which can be compiled without errors. Flowcharts charts can be thought of as a graphical alternative to pseudo code.
While writing pseudo codes, it is important to
keep in mind the precedence of operators (including arithmetic, relational and
logical operators). Generally, expressions involving such operators are
evaluated left-to-right following some precedence of operators just like the
BODMAS (hierarchy of arithmetic operators) concept you used to follow while
simplifying the algebraic expressions in your lower classes. For instance,
consider the precedence of most commonly used arithmetic operators, viz.,
addition, subtraction, multiplication and division. The addition and
subtraction operators have same precedence, whereas multiplication and division
operators have same precedence. However, level of precedence for multiplication
and division operators is higher than that for the addition and subtraction
operators. Hence, the following two expressions (on Right Hand Side (RHS) of
‘=’ symbol) would evaluate to two different results:
![]() and
and
![]() .
.
Note that parentheses are used to alter the normal order of evaluation. A complete discussion is given later in perspective with the ‘C’ programming.
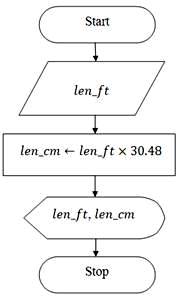
Example 1: Write an algorithm and a pseudo code as well as draw a flowchart to convert the length in feet to centimetre. Given that one foot contains 30.48 cm. (See Example-1 of Lesson-9 for the ‘C’ code corresponding to the following pseudo code).

Flowchart
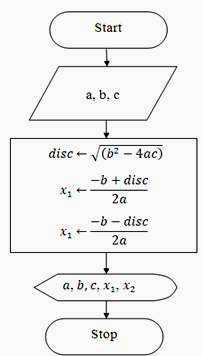
Example 2: Write an algorithm and draw a flowchart that will calculate the real roots of a quadratic equation. (See Example-2 of Lesson-9 for the ‘C’ code corresponding to the following pseudo code).

Flowchart
Example 3: The following algorithm inputs a student’s marks for four subjects; determines final grade by calculating the average of the four marks; and displays whether he/she is passing or failing on the basis that grade more than or equal to 50 is considered as ‘pass’, otherwise it is treated as ‘fail’.
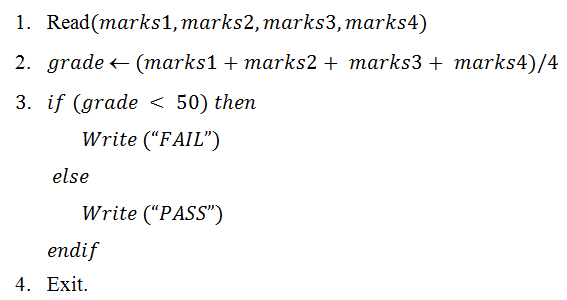
The students are advised to draw a flowchart and write a pseudo code for the above algorithm.
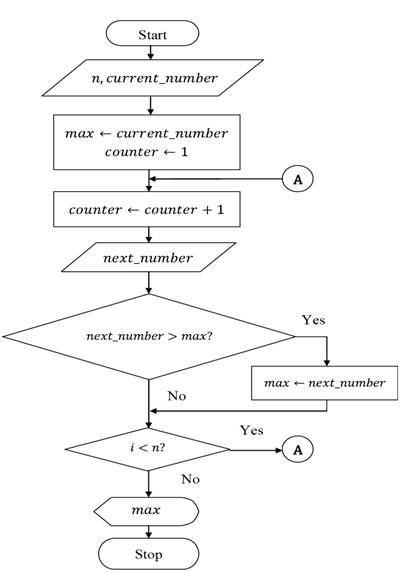
Example 4: Consider the algorithm developed in
Example-3 of Lesson-1. Write a pseudo code and draw corresponding
flowchart to find and print the largest number among any n given numbers.
1. Use
the variables n, current_number, next_number,
max and counter of the
type integer.
2. Input
values for n and current_number
3. max
= current_number
4. counter =1
5. while
condition (counter < n) holds good, do the following
i)
counter = counter +1
ii) Input next_number
iii) if (next_number>
max) then
max = next_number
(Note: previous value of max is
overwritten);
else
loop (i.e., go to step-5)
end if
end while
6. Print max with the preceding slogan, ‘The largest number is :’
7. End programme.
The flowchart
corresponding to the above pseudo code that finds and prints the largest number
among any n given numbers is given
below:
Example 5: Write a
suitable pseudo code and draw flowchart corresponding to the algorithm given in
Example-1(d) of Lesson-1 to compute average of any ten numbers using for loop.

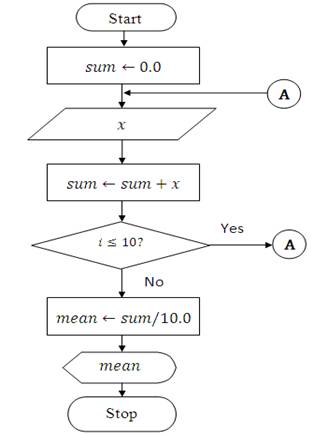
Example 6: Pesudo code to sort given set of numbers in ascending order
using the insertion sort method.
Suppose x is an array
of n values. We want to sort x in ascending order.
Insertion sort is an algorithm to do this. We traverse the array and insert
each element into the sorted part of the list where it belongs. This usually
involves pushing down the larger elements in the sorted part. The pseudo code
segment is as follow:

In above pseudo code, the phrase length (A) denotes a way (which may
be different for different programming languages; this may be even input by
user at the run-time of the progrmme) of getting
length of the array variable A. The ‘C’ function and complete programme for above
pseudo code is given in Example-2 of Lesson-15.
2.2 Analysis of Algorithms
The analysis of algorithms is the determination of
the amount of resources (such as time and storage) necessary to execute them.
Most algorithms are designed to work with inputs of arbitrary length. Usually
the efficiency or running time of an algorithm is stated as a function relating
the input length to the number of steps (i.e., time complexity) or
storage locations (i.e., space complexity).
Algorithm analysis is an important part of a
broader computational complexity theory, which provides theoretical estimates
for the resources needed by any algorithm that solves a given computational
problem. These estimates provide an insight into reasonable directions of
search for efficient algorithms.
2.3
Practical Exercises for Lesson 2
1. The following
flowchart depicts a programme that reads two given numbers; compares the two
numbers; and finally, displays the numbers read in decreasing order:

Write an equivalent
algorithm as well as pseudo code for the above flowchart.
2. Design an algorithm and
the corresponding flowchart and pseudo code for adding the test scores as given
below:
![]()
3. Write an algorithm and
pseudo code, which accepts two numbers from the keyboard; calculates the sum
and product of these numbers; and displays the results on the monitor’s screen.
4. Write a flowchart and an algorithm
that will output the square root of any positive number input from the keyboard
until the number input is zero.
5. Design an algorithm and
the corresponding pseudo code as well as flowchart for finding the sum of the
numbers: 2,4,6,8…n.
6. Write an algorithm and
draw a flowchart that will read the two sides of a rectangle and calculate its
area.