Module 1. Descriptive statistics

Lesson 4

MEASURES OF DISPERSION

4.1 Introduction

In the preceding lesson, we have seen different measures of central tendency and learnt how they can be calculated for varying types of distributions. The measures of central tendency are just different types of averages and do not indicate the extent of variability in a distribution. Averages or the measures of central tendency give us an idea of the concentration of the observations about the central part of the distributions. If we are given the average of a series of observations, we cannot form complete idea about the distribution since there may exist a number of distributions whose averages are same but they may differ widely from each other in a number of ways. Let us consider two series I and II of 6 items each

Series Total Mean

I 20 20 25 25 30 30 150 25

II 15 20 25 25 30 35 150 25

We notice that there is no difference as far as the average is concerned. But we notice that in the first case the observations vary from 20 to 30 and in the second case, the observations vary from 15 to 35 i.e. we notice that the greatest deviation from the mean in the first case is 5 and in the second case it is 10. Clearly this indicates a difference in the two series. Such a variation is called scatter or dispersion. Thus, the measures of central tendency must be supported and supplemented by some other measures. One such measure is dispersion. Measures of dispersion help us to study variability of the items i.e. the extent to which the items vary from one another and also from the central value.

4.2 Meaning of Dispersion

The term dispersion is generally used in two senses. Firstly, dispersion refers to the variation of the items among themselves. If the value of all the items of a series is the same, there will be no variation among the various items and the dispersion will be zero. On the other hand, the greater the variation among different items of a series, the more will be the extent of dispersion. Secondly, dispersion refers to the variation of the items about an average. If the difference between the value of items and the average is large, the dispersion will be high and on the other hand if the difference between the values of items and average is small, the dispersion will be low. Thus, dispersion is defined as scatteredness around central value or the spread of the individual items in a given series. According to A. L. Bowley “Dispersion is the measure of the variation of the items”. Spiegel defined dispersion as “The degree to which numerical data tend to spread about an average value is called the variation or dispersion of the data”.

4.3 Objectives of Measuring Dispersion

The measures of dispersion are helpful in statistical investigation. Some of the main objectives of dispersion are:

To determine the reliability of an average.
To compare the variability of two or more series.
For facilitating the use of other statistical measures.
Basis of Statistical Quality Control.

4.4 Characteristics for an Ideal Measure of Dispersion

The following are the essential requisites for an ideal measure of dispersion:

· It should be rigidly defined.

· It should be based on all observations.

· It should be readily comprehensive.

· It should be easily calculated.

· It should be amenable to further mathematical treatment.

· It should be affected as little as possible by fluctuations of sampling.

· It should not be affected much by extreme observations.

4.5 Absolute and Relative Measures of Dispersion

The measures of dispersion which are expressed in terms of the original units of a series are termed as Absolute Measures. Such measures are not suitable for comparing the variability of the two distributions which are expressed in different units of measurement. On the other hand, relative measures of dispersion are obtained as ratios or percentages and are thus pure numbers independent of the units of measurement. These measures are used to compare two series expressed in different units.

4.6 Measures of Dispersion

Various measures of dispersion in common use are:

4.6.1 Range

The simplest possible measure of dispersion is the range which is nothing but the difference between the greatest and the smallest observation of the distribution. Thus, Range =X_max -X_min where X_max is the greatest observation and X_minis the smallest observation of the variable value. In case of the grouped frequency distribution range is defined as the difference between upper limit of the highest class and the lower limit of the smallest class. In order to compare the variability of the two or more distributions given in different units of measurement, the relative measure , called coefficient of range is used and this is defined as follows:

In other words coefficient of range is the ratio of the difference between two extreme observations of the distribution to their sum.

4.6.1.1 Merits and demerits of range

Range is the simplest though crude measure of dispersion. It is rigidly defined, readily comprehensible and easiest to compute. It got the following drawbacks

It is not based on all the observations.
It is very much affected by fluctuations of sampling.
It is unreliable measure of the dispersion.
It cannot be used if we are dealing with open end classes.
Range is not suitable for mathematical treatment.

4.6.1.2 Uses of range

In spite of above limitations range as a measure of dispersion, has following applications

In a number of fields where the data have small variations like in stock market fluctuations, the variations in money rates and rate of exchange .
It is used in industry for the statistical quality control of the manufactured products by the construction of R chart i.e. the control chart for range.
It is also used as a very convenient measure by meteorological department for weather forecasts.

4.6.2 Quartile deviation or semi-inter-quartile range

The difference between the upper and lower quartiles i.e. Q₃ – Q₁ is known as the inter-quartile range and half of this difference i.e. (Q₃ – Q₁) is called the semi-inter-quartile range or the quartile deviation denoted by Q.D. For comparative studies of variability of two distributions the relative measure which is known as Coefficient of Quartile deviation which is given by

4.6.2.1 Merits of quartile deviation

The quartile deviation is easy to compute and understand.
It is a better measure of dispersion than range because it makes use of 50% of the data.
It is not affected at all by extreme observations.
It can be computed from the frequency distribution with open end classes.

4.6.2.2 Demerits of quartile deviation

It is not based on all the observations.
It is affected considerably by fluctuations of sampling.
It is not suitable for further mathematical treatment.

4.6.3 Mean deviation or average deviation

This measure of dispersion is obtained by taking the arithmetic mean of the absolute deviations of the given values from a measure of central tendency. According to Clark and Schkade: “Average deviation is the average amount of scatter of the items in a distribution either the mean or the median, ignoring the signs of deviations. The average that is taken of the scatter is an arithmetic mean, which accounted for the fact that this measure is often called the mean deviation”.

4.6.3.1 Calculation of mean deviation

If X₁, X₂, ---, X_n are n given observations then mean deviation (M.D.) about an average A is given by:

M.D. (about an average A) = Where read as mod (X_i-A) is the modulus value or absolute value of the deviation and A is one of the averages viz., Mean (M), Median (M_d) and Mode (M_o)

In case of grouped frequency distribution, mean deviation about an average A is given by:

M.D. (about an average A) = where X_i is the mid value of the class interval, f_i is the corresponding frequency, is the total frequency.

Mean deviation is minimum when it is calculated from median. In other words, mean deviation calculated about median will be less than the mean deviation about mean or mode. The relative measures of mean deviation is called coefficient of mean deviation is given by

The coefficients of mean deviations defined above are pure numbers independent of units of measurement and are useful for comparing the variability of different distributions. The calculation of various measures is illustrated in example 1.

Example 1: Find mean deviation from mean, median and mode using the data given in example 1 of Lesson 2. Also find the coefficient of mean deviation about mean, median and mode.
Solution : Using the values of Mean (M) =1910 Median (M_d) = 1890.8696 and Mode (M_o) = 1866.3636, calculated in Lesson 3and then prepare the following table:

Class Interval	Mid-value (X_i)	frequency (f_i)	X_i-M		X_i-M_d		X_i-M_o
1630-1730	1680	17	-230	3910	-210.87	3584.7832	-186.364	3168.1812
1730-1830	1780	19	-130	2470	-110.87	2106.5224	-86.3636	1640.9084
1830-1930	1880	23	-30	690	-10.8696	250.0008	13.6364	313.6372
1930-2030	1980	16	70	1120	89.1304	1426.0864	113.6364	1818.1824
2030-2130	2080	14	170	2380	189.1304	2647.8256	213.6364	2990.9096
2130-2230	2180	7	270	1890	289.1304	2023.9128	313.6364	2195.4548
2230-2330	2280	2	370	740	389.1304	778.2608	413.6364	827.2728
2330-2430	2380	2	470	940	489.1304	978.2608	513.6364	1027.2728
Total		100		14140		13795.6528		13981.8192

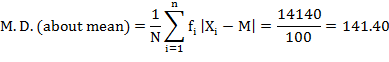
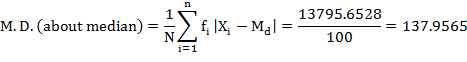
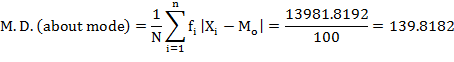
From above calculations we can verify that mean deviation calculated about median (137.9565) is less than mean deviation about mean (141.10) or mode (139.8182).

4.6.3.2 Merits of mean deviation

· It is rigidly defined, easy to understand and calculate.

· It is based on all observations and is better than range and quartile deviation.

· The averaging of the absolute deviations from an average irons out the irregularities in the distribution and thus provides an accurate measure of dispersion.

· It is less affected by extreme observations.

4.6.3.3 Demerits of mean deviation

· Ignoring the signs is not correct from mathematical point of view.

· It is not an accurate method when it is calculated from mode.

· It is not capable of further mathematical treatment.

· It cannot be used if we are dealing with open end classes.

4.6.4 Standard deviation

Standard deviation, usually denoted by the Greek alphabet σ was first suggested by Karl Pearson as a measure of dispersion in 1893. It is defined as the positive square root of the mean of the square of the deviations of the given observations from their arithmetic mean. If X₁,X₂,---, X_n is a set of n observations then its standard deviation is given by :

is the arithmetic mean.

In case of a grouped data, the standard deviation is given by:

Thus

Where;

X_i is the value of the variable or mid value of the class in case of grouped frequency distribution;

f_i is the corresponding frequency of the value X_i,

is the total frequency

is the arithmetic mean of the distribution.

The square of the standard deviation viz., σ² is called variance or second moment about mean.

4.6.4.1 Computation of variance (Direct method)

Other formulae for calculating variance is

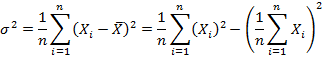
and in case of grouped data is

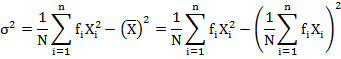
4.6.4.2 Short–cut method (Change of origin)

This method consists in taking deviations of the given observations from any arbitrary value A. The formula for calculation of the arithmetic mean is

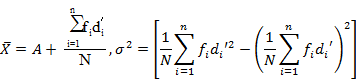
The variance and consequently the standard deviation of a distribution is independent of the change of origin. Thus, if we add (subtract) a constant to (from) each observation of the series, its variance remains same.

4.6.4.3 Step- deviation method (Change of origin and scale)

In case of grouped frequency distribution, with class intervals of equal magnitude, the calculations are further simplified by taking; where X_i is the mid value of the class and h is the common magnitude of the class intervals. So the formula for calculating mean and variance is

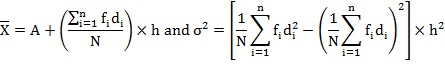
which shows that the variance or standard deviation is not independent of change of scale. Thus, if we multiply (divide) each observation of the series by a constant h, its variance will be multiplied (divided) by h².Hence variance and consequently the standard deviation of a distribution is independent of the change of origin but not of the scale. The procedure is illustrated in the example 2.It will be seen that the answer in each of the three cases is the same. The step-deviation method is the most convenient on account of simplified calculations.

Example 2: Find variance of the data given in example 1 of Lesson 3 with short-cut and step-deviation method.

Solution: Prepare the following table to calculate variance by different methods.

Class Interval	Mid-value (X_i)	freq (f_i)	f_iX_i	f_iX_i²	d_i’=X_i-A A=2080	f_id_i’	f_id_i’²		f_id_i	f_id_i²
1630-1730	1680	17	28560	47980800	-400	-6800	2720000	-4	-68	272
1730-1830	1780	19	33820	60199600	-300	-5700	1710000	-3	-57	171
1830-1930	1880	23	43240	81291200	-200	-4600	920000	-2	-46	92
1930-2030	1980	16	31680	62726400	-100	-1600	160000	-1	-16	16
2030-2130	2080	14	29120	60569600	0	0	0	0	0	0
2130-2230	2180	7	15260	33266800	100	700	70000	1	7	7
2230-2330	2280	2	4560	10396800	200	400	80000	2	4	8
2330-2430	2380	2	4760	11328800	300	600	180000	3	6	18
Total		100	191000	367760000		-17000	5840000		-170	584

Direct Method

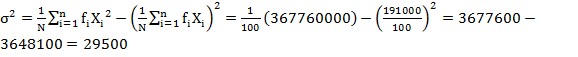
Short–cut Method

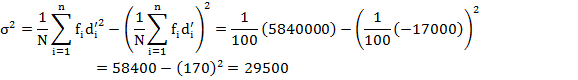
Step –Deviation Method

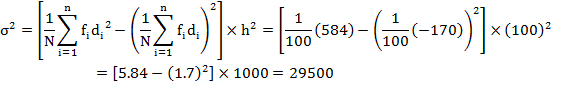
4.6.4.4 Merits of standard deviation

· It is rigidly defined.

· It is based on all observations and is the best measure of dispersion.

· The squaring of the deviations from mean removes the drawback of ignoring the signs of deviations in computing the mean deviation. This makes it suitable for further mathematical treatment. The variance of the combined series can also be computed.

· It is least affected by fluctuations of sampling and therefore, it widely used in sampling theory and tests of significance.

4.6.4.5 Demerits of standard deviation

· As compared to the quartile deviation and range etc., it is difficult to understand and difficult to calculate.

· It gives more importance to extreme observations.

4.6.4.6 Variance of the combined series

As pointed earlier variance is suitable for algebraic treatment i.e. if we are given the averages, the sizes and the variances of a number of series, then we can obtain the variance of the resultant series obtained by combining different series. Thus if are the variances; and are the arithmetic means and sizes of k series respectively . Then the variance of the combined series of size N= is given by the formula

Where

is the mean of combined series. In particular, for two series the combined variance is given by

Where

Substituting the values of and , combined variance is

4.6.5 Coefficient of variation

Standard deviation is an absolute measure of dispersion. The relative measure of dispersion based on standard deviation is called the coefficient of standard deviation and is given by

This is a pure number independent of the units of measurement and thus, is suitable for comparing the variability, homogeneity or uniformity of two or more distributions.

100 times the coefficient of dispersion based on standard deviation is called the coefficient of variation (C.V.) expressed in percentage. Thus,

Coefficient of Variation =

This measure was suggested by Prof. Karl Pearson and according to him “Coefficient of variation is the percentage variation in mean, standard deviation being considered as the total variation in the mean”. For comparing the variability of two distributions we compute the coefficient of variation for each distribution. A distribution with relatively smaller C.V. is said to be more homogeneous or uniform or less variable or more consistent than the other and the series with relatively greater C.V. is said to be more heterogeneous or more variable or less consistent than the other.