Module 3. Probability distributions
Lesson 11
POISSON DISTRIBUTION
11.1 Introduction
Having discussed
the binomial distribution in the preceding lesson, we now turn to Poisson distribution,
which is also a discrete probability distribution. Before we know the
distribution, it becomes necessary to understand what a Poisson variable is. A
variable which can take only one discrete value in an interval of time, however
small, is known as Poisson variable. It was given by French Mathematician S. D.
Poisson (1781-1840) and hence named after him. When n is very very large (n→∞)
and p is very very small (p→0)
then binomial distribution cant be applied. As binomial distribution, Poisson distribution
is also one of the most widely used distributions .It is used in quality
control to count the number of defective items or in insurance problems to
count the number of causalities.
11.2
Poisson Distribution
Poisson distribution is a limiting case of Binomial distribution under the following conditions:
(i) n, the no. of trials is indefinitely large i.e., n→∞
(ii) p, the constant probability of success for each trial is indefinitely small i.e. p→0
(iii) np= m (say) is finite. Thus, p = m/n, q = 1m/n where m is a positive real number.
Under, the above three conditions the probability mass function of binomial distribution tends to the probability mass function of the Poisson distribution whose definition and derivation given below:
Definition: A random variable X is said to follow a Poisson distribution if it assumes only non-negative values and its probability mass function is given by
where m is known as the parameter of the distribution .
e = 2.7183(the base of the natural logarithm)
Proof: As n→∞
and np=m
p =
m/n and q=1-m/n
Probability
function of binomial distribution is
P (r) = nCr pr qn-r = n!/r!(n-r)! pr qn-r
Taking limit as n→∞
We know that
Putting
r = 0,1,2, ---- in above equation, we obtain the
probabilities of r = 0,1,2, ---- successes respectively we get 
, 
,
,---
Total
probability is 1:
----
=
If we know m, all the probabilities of the Poisson distribution can be obtained, therefore m is the only parameter of the Poisson distribution. The application of this distribution in solving problems is illustrated through following examples.
Example 1. A manufacturer of screws knows that 5% of his product is detective. If he sells his product in a carton of 100 items and guarantees that not more than 10 items will be defective. What is the probability that the carton will fail to meet the guaranteed quality?
Solution:
In this example p = 0.05, n = 100. Therefore, m = n. p = 100 (0.05) = 5
Prob. [That the carton will fail to meet the guaranteed quality] = 1 Prob. [The carton will meet the guaranteed quality] = Prob. [Not more than 10 items will be defective] = 1 P [r ≤ 10]
= 1- [P(0) + P(1) + P(2) + P(3)+ + P(10)]
In case of Poisson distribution 
Therefore, we have P(r > 10) = 1 P(r ≤
10) = 1 - 
=
Example 2. A milk plant manufacturing ghee pouches; there are small chances of 1/500 for any ghee pouch to be defective. These pouches are supplied in packet of 10. What will be the approximate number of pouches containing no defective, one defective, two defective and three defective ghee pouches in a consignment of 5,000 pouches?
Solution:
In this exercise p = 1/500, n = 10 therefore m = 10/500 = 0.002
Prob. [Packet
containing no defective] = 
Prob. [Packet
containing one defective] = 
Prob. [Packet
containing two defective] = 
Prob. [Packet
containing three defective] = 
Therefore, the expected number of pouches containing no defective, one defective, two defective, and three defective ghee pouches in a consignment of 5000 pouches.
E(0) = N P(0) = 5000 (0.9802) = 4901
E(1) = N P(1) = 5000 (0.0196) = 98
E(2) = N P(2) = 5000 (0.0002) = 1
E(3) = N P(3) = 5000 (0) = 0
11.3 Examples of Poisson Distribution
· The number of defective milk pouches per lot.
· The number of deaths of cattle in big dairy farm in one year by a rare disease.
· Number of bottles broken in different months or bottle breakage during different months.
· The number of bacterial colonies in a given culture per unit area of microscope.
· Number of suicides reported in a particular city.
· Number of defective material in a packaging manufactured by a good concern.
· Number of printing mistakes at each page of the book.
· Number of deaths from a disease (not in the form of epidemic) such as heart attack or cancer or snake bite.
· The emission of radioactive (alpha) particles. A small mass of radian contain many millions of atoms.
· Number of fragments received by a surface area t from a fragment of atom bomb
11.4 Properties of Poisson Distribution
i) Mean of the Poisson distribution is m
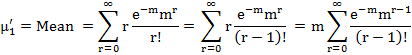
ii) Variance of the Poisson distribution is
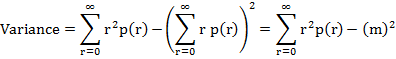
where,
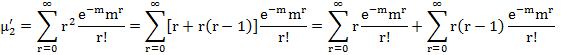
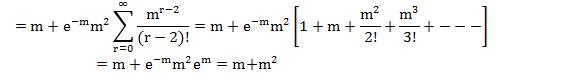
= m
Hence, for Poisson distribution with parameter m mean is equal to variance.
iii) Third and fourth central moments ΅3 and ΅4
iv) Pearsons
constants β1 & β2 as well as γ1
and γ2 are given by
It
may be noted that the first three central moments of the Poisson distribution
are identical and are equal to the value of parameter itself namely m. Hence
Poisson distribution is always a positively skewed distribution as m>0 as
well as leptokurtic. As the value of m increases γ1
decreases and
the thus skewness is reduced for increasing values of
m. As m⟶∞, γ1 and γ2 tend to zero. So we conclude
that as m⟶∞, the curve of the Poisson
distribution tends to be symmetrical curve for large values of m.
v) Mode of Poisson distribution is determined by the value m. If m is an integer then the distribution is bi-modal, the two modal values being X=m and X=m-1.When m is not an integer then the distribution has unique modal value being integral part of m.
vi) Additive property: If X1 and X2 are two independent Poisson variate with parameters m1 and m2 then their sum X1 + X2 is also a Poisson variate with parameter m1 + m2.
Example 3. The mean of the Poisson distribution is 2.25. Find the other constants of the distribution.
Solution:
We have 
This curve is positively skewed and leptokurtic.
Example 4. In a Poisson distribution 3P (X = 2) = P (X = 4). Find P (X = 3)
Solution:
Since 3P(X = 2) = P(X = 4)
Example 5.
A discrete random variable X follows a Poisson distribution. Find
i) P(X ≥ 3) and ii) P (X is
at most 2), if it is given E (X) = 3 and 
Solution:
Here m
= 3,
i) P (X ≥ 3) = 1 - [P (X = 0) + P (X = 1) + P(X = 2)]
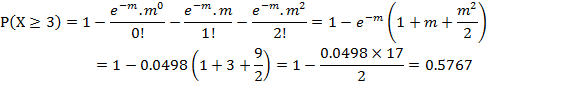
ii) 
11.5 Fitting of Poisson Distribution
If we want
to fit a Poisson distribution to a given frequency distribution, we compute
mean of the given frequency distribution by the formula 
and equate
it to m which is mean of the Poisson distribution. Once m is known, the various
probabilities can be calculated by the formula
If N is the total observed frequency, then the expected or theoretical frequencies of the Poisson distribution are given in the following table.
|
No. of successes ( r ) |
Expected or theoretical Frequencies. N.P(r) |
|
0 |
N |
|
1 |
N m |
|
2 |
N |
|
: |
: |
|
r |
N |
|
: |
: |
The expected frequencies can also be computed by using the following recurrence formula
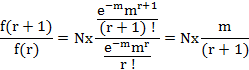
The procedure is illustrated through following examples.
Example 6. The following table gives the number of lactations completed by 1000 cows of Tharparkar breed:
|
No. of lactations (Xi) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
No. of cows |
300 |
205 |
155 |
126 |
90 |
47 |
35 |
18 |
13 |
8 |
3 |
Fit a Poisson distribution to the above data.
Solution: In the usual notations we have:
N=1000, 
=2030,
putting
r=0,1,2,3,---,10 in 
we get the
expected as given in the following table:
|
No. of lactations completed (Xi) |
No. of cows (fi) |
fi Xi |
Expected Frequency E(r) |
|
0 |
300 |
0 |
131.3355 |
|
1 |
205 |
205 |
266.6111 |
|
2 |
155 |
310 |
270.6103 |
|
3 |
126 |
378 |
183.1130 |
|
4 |
90 |
360 |
92.9298 |
|
5 |
47 |
235 |
37.7295 |
|
6 |
35 |
210 |
12.7652 |
|
7 |
18 |
126 |
3.7019 |
|
8 |
13 |
104 |
0.9394 |
|
9 |
8 |
72 |
0.2119 |
|
10 |
3 |
30 |
0.0430 |
|
Total |
1000 |
2030 |
999.9905 |
Different expected frequencies are also computed by using recurrence formula
E(0)=1000 Χ e-2.03 = 131.3355;
E(1)=2.03 Χ 131.3355 = 266.6111;
E(2)=2.03/2 (266.6111) = 270.6103;
E(3)=2.03/3 (270.6103) = 183.1130;
E(4)=2.03/4 (183.1130) = 92.9298;
E(5)=2.03/5 (92.9298) = 37.7295;
E(6)=2.03/6 (37.7295) = 12.7652;
E(7)=2.03/7 (12.7652) = 3.7019;
E(8)=2.03/8 (3.7019) = 0.9394;
E(9)=2.03/9 (0.9394) = 0.2119;
E(10)=2.03/10 (0.2119) = 0.0430