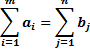Module 3. Transportation problems

Lesson 5

DEFINITION AND MATHEMATICAL FORMULATION

5.1 Introduction

The Transportation Problem (TP) is a special type of LP problem where the objective is to minimize the cost of distributing a single commodity from a number of supply sources (e.g. factories) to a number of demand destinations (e.g. warehouses). The objective of the problem is to determine the amount to be transported from each source to each destination so as to maintain the supply and demand requirements at the lowest transportation cost. The characteristic of a TP are such that it is usually solved by a specialized method rather than by simplex method. A key problem in many projects is the allocation of scarce resources among various activities. TP refers to a planning model that allocates resources, machines, materials, capital etc. in the best possible manner so that the costs are minimized or profits are maximized.

5.2 Formulation of Transportation Problem

Transportation problem is an important class of the linear programming problem in which, the objective is to transport various quantities of a single homogenous commodity that are stored at various origins to different destinations in such a way that the transportation cost is minimum. Transportation problem arises in situations involving physical movements of goods e.g. milk and milk products from plants to cold storages, cold storages to wholesalers, wholesalers to retailers and retailers to customers. The solution of a TP is to determine the quantity to be shifted from each plant to each cold storage so as to maintain the supply and demand requirements at the lowest transportation cost.  

Let us suppose that there are m origins (dairy plants) supplying a certain homogeneous dairy product to n destinations (cold storages). Let plant P_i (i = 1, 2, …,m) produce a_i units and cold storage W_j (j = 1, 2,. . ., n) requires b_j units. Suppose that the cost of transporting from plant Pi to cold storage W_j is directly proportional to the amount/quantity transported and let C_ij be the cost of transporting one unit of product from i^th origin to j^th destination and   X_ij be the amount/quantity transported from i^th origin to j^th destination. The objective is to determine the number of units to be transported from i^th origin to j^th destination such that the transportation cost is minimized. For balanced transportation problem, it is assumed that the total supply equals to the total demand. The transportation problem in a tabular form can be represented as follows:

Table 5.1 Tabular representation of transportation problem

Dairy Plants/ Sources	Warehouses (Cold storage)/Destinations							Dairy Plant Capacity
	W1	W2	…..	…..	Wj	…..	Wn
P1			….	….		……		a1
P2			….	…...		…..		a2
:	:	:	:	:	:	:		:
Pi			:	:		:		ai
:	:	:	:	:	:	:		:
Pm			….	….		……		am
Cold storage Requirements	b1	b2	….	…..	bj	…..	bn

Where C_ij and X_ij are unit cost of transportation and quantity transported respectively in the cell (i, j). Then the sum of the product of X_ij and C_ij of allocated cells

gives us the net cost in transporting X_ij units from plant Pi to cold storage W_j. 

The following example will help to demonstrate the formulation of the transportation problem:

Example 1

Milk in a milk shed area is collected on three routes A, B and C. There are four chilling centers P, Q, R and S where milk is kept before transporting it to a milk plant. Each route is able to supply on an average one thousand litres of milk per day. The supply of milk on routes A, B and C are 150, 160 and 90 thousand litres respectively.  Daily capacity in thousand litres of chilling centers is 140, 120, 90 and 50 respectively. The cost of transporting 1000 litres of milk from each route (source) to each chilling center (destination) differs according to the distance. These costs (in Rs.) are shown in the following table:

Routes	Chilling centers
	P	Q	R	S
A	16	18	21	12
B	17	19	14	13
C	32	11	15	10

The problem is to determine how many thousand liters of milk is to be transported from each route on daily basis in order to minimize the total cost of transportation.

Solution

A transportation problem can be formulated as a linear programming problem. To illustrate this, let us see how this example can be formulated as a linear programming problem. Let X_ij represent the quantity transported from i^th route to j^th chilling center. These are the decision variables. In this example there are twelve decision variables. Let C_ij represents the cost of transported thousand litres of milk from i^th route to j ^th chilling center. The objective is to find the values for the X_ij so as to minimize total transportation cost. Thus the LP objective function is:

The supply of milk on routes A, B and C and daily capacity in thousand litres of chilling centers P, Q, R and S impose constraints. The total quantity transported from route A must be equal to its capacity i.e. 150 thousand litres milk. Thus, for route A, the constraint is:

Similarly, the constraint for other two routes B and C can be expressed as under:

Similarly, we must satisfy the demand for each of the four chilling centers. The units can be transported through route A, B and C. Thus, for Chilling centre P, the constraint is:

Similarly, constraints for the other three chilling centers Q, R and S

Finally, all values of X_ij must be greater than or equal to zero, as negative units cannot be transported. Thus, X_ij ≥ 0 for i=1,2,3 ; j=1,2,3,4.

Thus the linear programming formulation of the transportation problem becomes:

Subject to

Supply constraints	Demand Constraints

And X_ij ≥ 0 for i=1,2,3 ; j=1,2,3,4. 

5.3  Mathematical Formulation of the Transportation Problem

Using the notations described in the previous section, the transportation problem consist of finding X_ij (i =1, 2, . . ., m; j=1, 2, . . , n) in order to minimize the total transportation cost . It is assumed that the total availabilities equals to the total requirements i.e. (rim condition). The problem now is to determine non–negative values of X_ij (≥0) which satisfy both the availability constraints and requirement constraints .

Such types of problems where supply and demand are exactly equal are known as Balanced Transportation Problem. Supply (from various sources) is written in the rows, while a column is an expression for the demand of different warehouses. In general, if a transportation problem has m rows and n columns, then the problem is solvable if there are exactly (m + n –1) basic variables. However, a transportation problem is unbalanced if the total supply and the total demand are not equal.