Module 2. Theory of probability
Lesson 7
ADDITION THEOREM OF PROBABILITY
7.1 Introduction
In the last lesson we have studied the probability of an event in a random experiment as well as axiomatic approach formulated by Russian Mathematician A.N. Kolmogorov and observed that probability as a function of outcomes of an experiment. By now you know that the probability P(A) of an event A associated with a discrete sample space is the sum of the probabilities assigned to the sample points in A as discussed in axiomatic approach of probability. Moreover, in practical problems, writing down the elements of S and counting the number of cases favourable to a given event often become very tedious. However in such situations the computation of probabilities can be facilitated to a great extent by fundamental theorem of addition. In this lesson we will learn Addition Theorem of Probability to find probability of occurrence for simultaneous trials under two conditions when events are mutually exclusive and when they are not mutually exclusive.
7.2 List
of Symbols
A∪B:
An event which represents the happening of at least one of the events A and B
i.e. either A occurs or B occurs or both A and B occur. This is also denoted as
A or B
A∩B: An event which represents the simultaneous happening of both A and B i.e. A and B.
![]() A
does not happen.
A
does not happen.
![]() Neither A nor B happens i.e. none of A and B
happens.
Neither A nor B happens i.e. none of A and B
happens.
![]() A does not happen but B happens.
A does not happen but B happens.
![]() Exactly one of the two events A and B happens.
Exactly one of the two events A and B happens.
7.3 Addition Theorem for Mutually Exclusive Events
Statement: If A and B are two mutually exclusive events, then the probability of occurrence of either A or B is the sum of the individual probabilities of A and B. Symbolically
![]()
Proof : Let N be the total number exhaustive and equally likely cases of an experiment. Let m1 and m2 be the number of cases favourable to the happening of events A and B respectively. Then
![]()
and
![]() .
.
Since the events A and B are mutually exclusive, the total number of events favorable to either A or B i.e. n(A∪B) = m1+m2, then
![]()
Generalisation: This theorem can be extended to three or more mutually exclusive events. The probability of occurrence of any one of the several mutually exclusive events A, B and C is equal to the sum of their individual probabilities given by
![]()
In general, if A1, A2 … An are mutually exclusive events then
![]()
i.e., the probability of occurrence of any one of the n mutually disjoint events A1, A2 … An is equal to the sum of their individual probabilities.
The following examples illustrate the application of this theorem:
Example 1: A card is drawn at random from a pack of 52 cards. Find the probability that the drawn card is either a club or an ace of diamond.
Solution : Let A : Event of drawing a card of club and
B: Event of drawing an ace of diamond
The
probability of drawing a card of club ![]()
The
probability of drawing an ace of diamond ![]()
Since the events are mutually exclusive, the probability of the drawn card being a club or an ace of diamond is:
![]()
Example 2: A herd contains 30 cows numbered from 1 to 30. One cow is selected at random. Find the probability that number of the selected cow is a multiple of 5 or 8.
Solution: Let A be the event of number being a multiple of 5 within 30 and B be the event of number being a multiple of 8 within 30.
Favourable cases for event A are {5, 10, 15, 20, 25, 30}
Similarly favourable cases for event B are {8, 16, 24}
The
probability of the number being a multiple of 5 within 30 is P (A) =![]()
The
probability of the number being a multiple of 8 within 30 is P (B) =![]()
Since A and B are mutually exclusive, the probability that number of the cow is a multiple of 5 or 8 is:
![]()
7.4 Addition Theorem for Non-mutually Exclusive Events
The addition theorem discussed above is not applicable when the events are not mutually exclusive. For example, if one card is drawn at random from a pack of 52 cards then in order to find the probability of either a spade or a king card, it cannot be calculated by simply adding the probabilities of spade and king card because the events are not mutually exclusive as there is one card which is a spade as well as a king. Thus, the events are not mutually exclusive; therefore, the addition theorem is modified as:
Statement: If A and B are not mutually exclusive events, the probability of the occurrence of either A or B or both is equal to the probability that event A occurs, plus the probability that event B occurs minus the probability of occurrence of the events common to both A and B. In other words the probability of occurrence of at least one of them is given by
![]()
Proof: Let us suppose that a random experiment results in a sample space S with N sample points (exhaustive number of cases). Then by definition
![]()
Where n(A∪B) is the number of occurrences (sample points) favorable to the event (A∪B)
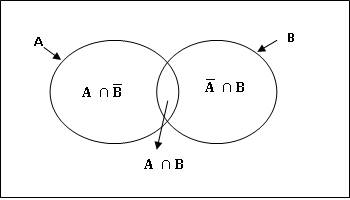
Fig. 7.1 Addition theorem for non-mutually exclusive events
From
the above diagram, we get:
![]()
![]()
![]()
![]()
Generalisation The above theorem can be extended to three or more events. If A, B and C are not mutually exclusive events then the probability of the occurrence of at least one of them is given by
![]()
![]()
![]()
![]()
If n mutually exclusive events A1, A2 … An are exhaustive also, so that probability of at least one of the n events to materialize is a certainty then the probability of the constituent events.
P(A1 + A2 + …….. + An) = 1
P(A1) + P(A2) + ………. + P(An) = 1
The following examples illustrate the application of this theorem:
Example 3. A card is drawn at random from a pack of 52 cards. Find the probability that the drawn card is either a spade or a king.
Solution: Let A: Event of drawing a card of spade and
B: Event of drawing a king card
The
probability of drawing a card of spade ![]()
The
probability of drawing a king card ![]()
Because one of the kings is a spade card
also therefore, these events are not mutually exclusive. The probability of
drawing a king of spade is ![]()
So, the probability of the drawing a spade or king card is:
![]()
Example 4. A herd contains 30 cows numbered from 1 to 30. One cow is selected at random. Find the probability that the number of the selected cow is a multiple of 5 or 6.
Solution: Let A be the event of number being a multiple of 5 within 30 and B be the event of number being a multiple of 6 within 30.
Favourable cases for event A are {5, 10, 15, 20, 25, 30}
Similarly favourable cases for event B are {6, 12, 18, 24, 30}
The
probability of the number being a multiple of 5 within 30 is P(A)=![]()
The
probability of the number being a multiple of 6within 30 is P(B)=![]()
Since 30 is a multiple of 5 as well as 6, therefore the events are not mutually exclusive
![]()
The probability that the number of the selected cow is a multiple of 5 or 6 is :
![]()
Example 5. A number was drawn at random from the number 1 to 50. What is the probability that it will be a multiple of 2 or 3 or 10?
Solution: Probability
of getting a multiple of 2: ![]()
Probability of getting a multiple of 3: ![]()
Probability
of getting a multiple of 10: ![]()
Common
Probability of getting a multiple of 2 and 3: ![]()
Common
Probability of getting a multiple of 3 and 10: ![]()
Common
Probability of getting a multiple of 2 and 10: ![]()
Common
Probability of getting a multiple of 2, 3 and 10: ![]()
Probability that it is a multiple of 2 or 3 or 10:
![]()
![]()