Module 4. Assignment problem

Lesson 8

INTRODUCTION AND MATHEMATICAL FORMULATION

8.1 Introduction

In earlier module, transportation problem and the technique of solving such a problem was discussed. In this lesson, the Assignment Problem, which is a special type of transportation problem, is introduced. Here the objective is to minimize the cost or time of completion of a number of jobs by a number of persons. In other words, when the problem involves the allocation of n different facilities to n different tasks, it is often termed as Assignment Problem. The assignment problem deals in allocating the various origins (jobs) to equal number of destinations (persons) on a one to one basis in such a way that the resultant effectiveness is optimized (minimum cost or maximum profit). This is useful in solving problems such as assigning men to different operations in a milk plant, milk tankers to delivery routes, machine operators to machines, jobs to persons in a dairy plant etc.

8.2 Definition of Assignment Problem

Assignment problem is special class of the transportation problem in which the supply in each row represents the availability of a resource such as man, vehicle, product and demand in each column represents different activities to be performed, such as jobs, routes, milk plants respectively is required. The name ‘Assignment Problem ’originates from the classical problem where the objective is to assign a number of origins (jobs) to equal number of destinations(persons) at a minimum cost (or Maximum profit). Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a time, though with varying degree of efficiency. Let C_ij be the cost if i^th person is assigned the j^th job, the problem is to find an assignment so that the total cost for performing all jobs is minimum. One of the important characteristics of assignment problem is that only one job (or worker) is assigned to one machine (or project). Hence, the number of sources are equal to the number of destinations and each requirement and capacity value is exactly one unit.

The assignment problem can be stated in the form n x n cost matrix [C_ij] of real number as given below

Sources (Milk plants)	Jobs
	J1	J2	……	Jj	……	Jn
P1	C11	C12	……	C1j	……	C1n
P2	C21	C22	……	C2j	……	C2n
:	:	:	……	:	……	:
Pi	Ci1	Ci2	……	Cij	……	Cin
:	:	:	……	:	……	:
Pn	Cn1	Cn2	……	Cnj	……	Cnn

Formulation of an Assignment Problem

Let us consider the case of a milk plant which has three jobs to be done on the three available machines. Each machine is capable of doing any of the three jobs. For each job the cost depends on the machine to which it is assigned. Costs incurred by doing various jobs on different machines are given below

Job	Machine
	I	II	III
A	7	8	6
B	5	4	9
C	2	5	6

The problem of assigning jobs to machines, one to each, so as to minimize total cost of doing all the jobs, is an assignment problem. Each job machine combination which associates all jobs to machines on one –to-one basis is called an assignment. In the above example let us write all the possible assignments

Number	Assignment	Total Cost
1	Job A-Machine I, Job B –Machine II, Job C-Machine III	7+8+6=21
2	Job A-Machine I, Job B –Machine III, Job C-Machine II	7+9+5=21
3	Job A-Machine II, Job B –Machine III, Job C-Machine I	8+9+2=19
4	Job A-Machine II, Job B –Machine I, Job C-Machine III	8+5+6=19
5	Job A-Machine III, Job B –Machine I, Job C-Machine II	6+5+2=13
6	Job A-Machine III, Job B –Machine II, Job C-Machine I	6+4+2=12

As per the above assignment, the assignment number 6 having total cost 12 is minimum therefore needs to be selected. But selecting assignment in this manner is quite time consuming.

8.3  Mathematical Formulation of Assignment Problem

Using the notations described above, the assignment problem consist of finding the values of X_ij in order to minimize the total cost

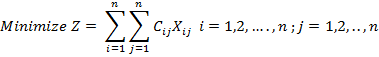
Subject to restrictions

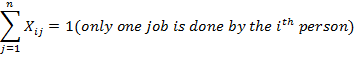
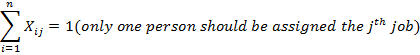
where X_ij denotes the j^th job to be assigned to the i^th person. An assignment problem could thus be solved by Simplex Method.

We state below, the following theorems which have potential applications in finding out of the optimal solution for assignment problems:

Theorem 1 Reduction Theorem

It states that in an assignment problem, if we add or subtract a constant to every element of any line (row or column) of the cost matrix [C_ij], then an assignment that minimizes the total cost on one matrix also minimizes the total cost on the other matrix.

Theorem 2 In an assignment problem with cost (C_ij), if all C_ij≥ 0 then a feasible solution (X_ij) which satisfies, is optimal for the problem

Remarks
There are situations when a particular assignment may not be permissible. In such situations assign a very high cost (say M) for such an assignment and proceed as usual.

1. If the assignment problem involves maximization, convert the effective matrix to an opportunities loss matrix by subtracting each element from the highest element of the matrix. Minimization of the resulting matrix is the same as the maximization of the original matrix.

8.4  Similarity of Assignment Problem to Transportation Problem

The assignment problem is a particular case of transportation problem in which a number of operations are to be assigned to an equal number of operators, where each operator performs only one operation. The objective is to maximize overall profit or minimize overall cost for a given assignment schedule.

The Assignment Problem is a special case of the transportation problem in which m=n, All a_i and b_j are unity i.e., The availability and requirement at i^th origin and j^th destination are unity, and each X_ij is limited to one of the two values 0 and 1. Under these circumstances, exactly n of X_ij can be non-zero (i.e., unity), one in each row of the table and one in each column.

An assignment problem is a completely degenerate form of a transportation problem. The units available at each origin and units demanded at each destination are all equal to one. This means exactly one occupied cell in each row and each column of the transportation table. i.e., only n occupied cells in place of the required (n + n – 1) = (2n – 1).