Module 2. A.C. series and parallel circuits

Lesson 6

A.C. SERIES AND PARALLEL CIRCUITS

6.1 A.C. Circuit

When an alternating current flows in closed loop or a path, it is called an a.c. circuit. Different elements of an a.c. circuit may be any or in combination of following:

1. Resistance: An electrical element which causes opposition to the passage of an electric current through that element.

2. Inductance: In electromagnetism and electronics, inductance in the circuit "induces" (creates) a voltage (electromotive force) in both the circuit itself (self-inductance) and any nearby circuits (mutual inductance). Inductance is typified by the behaviour of a coil of wire in resisting any change of electric current through the coil.

3. Capacitance: Capacitance is the ability of a body to store an electrical charge. Any element or structure that is capable of being charged, either with static electricity or by an electric current exhibits capacitance.

If the voltage applied to an a.c. circuit in sinusoidal, the resulting alternating current is sinusoidal. Also the frequency of the alternating current will be equal to that of applied voltage. The opposition to the flow of current in an a.c. circuit may be due to:

1. Resistance R

2. Inductive reactance (X_L= ωL)

3. Capacitive reactance (X_C= )

Different types of A.C. Circuit can be listed as follows:

1. A.C. Circuit with only one element

a) Resistance

b) Inductance

c) Capacitance

2. A.C. Series Circuit

a) R-L Series Circuit

b) R-C Series Circuit

c) R-L-C Series Circuit

3. A.C. Parallel Circuit

6.2 A.C. Circuit with Only One Element

6.2.1 A.C. Circuit with only one element-resistance

The figure 6.1 shows an a.c. circuit with a pure resistance of R Ω

Fig. 6.1 A.C. Circuit with only one element-Resistance

The current in the circuit is i = v/R ......... (1)

The instantaneous value of alternating voltage is given by:

v = V_mSin ωt ......... (2)

From equation (1) and (2)

......... (3)
The value of current will be maximum when Sin 𝜔t=1

......... (4)

From equation (3) and (4)

i = I_mSin ωt ......... (5)

In an a.c. circuit having resistance as any element, the phase difference between voltage and current is zero. In other words it can be said that current is in phase with the voltage power.

We know instantaneous power p = vi

From equation (2) and (5) we have

Considering average power

P = V_rmsI_rms

p = v i where V = rms voltage, I = rms current

6.2.2 A.C. Circuit with only one element-inductance

Figure 6.2 shows an a.c. circuit with pure inductance of L Henry

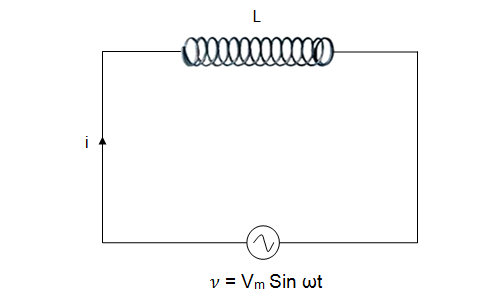
Fig. 6.2 A.C. Circuit with only one element-Inductance

The sinusoidal voltage can be given as

The e.m.f in the coil due to the current I flowing in the circuit can be given as

......... (2)

The induced e.m.f is also called e.m.f opposes the change of current in the coil .Back e.m.f. induced in the coil is equal and opposite of the applied voltage. Thus equation

Integrating

......... (3)

i will be maximum when value of ) is one

......... (4)

In the above equation

ωL is also known as inductive reactance X_L of the coil.

ω =angular velocity

f =frequency in hertz

L =inductance in henry

X_L=inductive reactance in Ω (ohms)

Note: X_Lis the opposition offered by pure inductance to the flow of an alternating current

From equation (3) and (4) we have

......... (5)

From equation (1) and (5) it can be seen that current in a inductive circuit lags behind the voltage by radians or 90^o.It is well represented in the phasor diagram shown in fig. 6.3

Fig. 6.3 Phasor diagram for current and voltage in an inductive circuit

Power

Instantaneous power p = v i

Average power consumed over one cycle

This shows that power absorbed in a circuit having only inductance element is zero

6.2.3 A.C. circuit with only one element- capacitance

Fig. 6.4 Shows a circuit with capacitance C farads

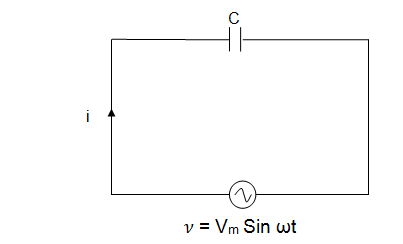
Fig. 6.4 Circuit with capacitance C farads

The value of alternating voltage is given as

The charge on the capacitor q=c v

The current in the circuit is

......... (1)

The value of the current will be maximum when

From equation (1)

This equation shows that in a circuit with capacitance as an only element, the current leads the voltage by 90^o (Fig. 6.5)

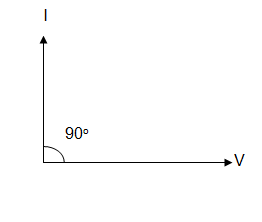
Fig. 6.5 Current leads the voltage by 90^o in a circuit with capacitance

Power

Instantaneous power is given by

p = v i

The average power over one complete cycle is p = Zero

The power absorbed in a circuit with pure capacitance is zero.

6.3 A.C. Series Circuit

There are three major types of circuit as follows

1. R-L Series Circuit

2. R-C Series Circuit

3. R-L-C Series circuit

6.3.1 R-L series circuit

Figure 6.6 shows a pure resistance and inductance connected in series

Fig. 6.6 A.C. circuit with series resistance and inductance

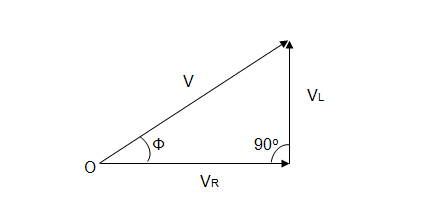
Fig. 6.7 Phasor diagram for a.c. series circuit

From the phasor diagram

V²= (V_R)²+ (V_L)²

Here,

V = r.m.s value of applied voltage

I = r.m.s. value of current

V_R= voltage drop across R = IR

V_L= voltage drop across L = IX_L

Z = Impedance of the circuit and it is measured in Ω ohms

Here ϕ is known as phase angle

Voltage leads current by ϕ angle. In other words it can be said that current lags voltage by ϕ angle. Figure 6.8 shows the impedance triangle

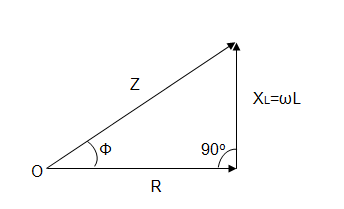
Fig. 6.8 Impedence triangle for a.c. series circuit

Impedance Z

Here, Z = Impedance and R = Resistance

X_L=Inductive reactance

ϕ = Phase angle

Cos ϕ = power factor of the circuit

Power P= VI Cos ϕ

= (Z.I) ICos ϕ

P = I²R

In a series R-L Circuit power is consumed in resistance only. Inductance consumes zero power. The unit of power is watt.

6.3.2 R-C series circuit

Fig. 6.9 shows a pure resistance and capacitance connected in series.

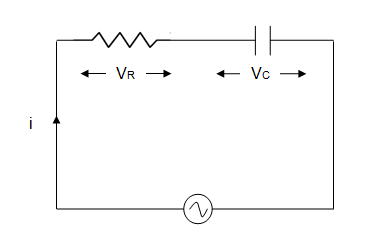
Fig. 6.9 A.C. circuit with series resistance and capacitance

Fig. 6.10 Phasor diagram for a.c. series resistance and capacitance circuit

From the phasor diagram figure 6.10

V²= (V_R)²+ (-V_C)²

Here,

V = r.m.s value of applied voltage

I = r.m.s. value of current

V_R= Voltage drop across R = IR

V_C= Voltage drop across C = IX_C

Z = Impedance of the circuit and it is measured in ohms

Here ϕ is known as phase angle.

Current leads voltage by ϕ angle. In other word can be said that voltage lags current by ϕ angle. The figure 6.11 shows the impedance triangle.

Fig. 6.11 Impedance triangle for a.c. series circuit

Impedance Z

Here, Z = Impedance and R=Resistance

X_C= Capacitive reactance

= Power factor of circuit

C = Capacitance

X_C= = Capacitive reactance

Power P = VICosϕ

Here,

V = r.m.s value of applied voltage

I = r.m.s. value of current

= Power factor of circuit

6.3.3 R-L-C series circuit

When a pure resistance R ohms, pure inductance L Henry and pure capacitor of capacitance C farad are connected in series it is known as R-L-C Series Circuit.

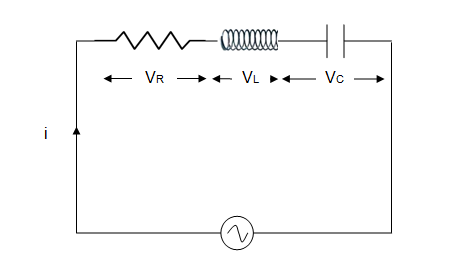
Fig. 6.12 A.C. series circuit for resistance, inductance and capacitance

Fig. 6.13 Phasor diagram for resistance, inductance and capacitance series circuit

The voltage drop across each element is given as:

a) Resistance (R) = V_R= IR (in phase with current I)

b) Inductance (L) = V_L= IX_L (leads current by 90^o)

c) Capacitance (C) = V_C= I.X_C( lags current by 90^o)

In the phasor diagram V_L is leading current I by 90^o and V_C is lagging current by 90o. So it is evident that V_L and V_C are at 180o to each other. In technical terms it is said to be 180o out of phase with each other. The circuit will behave like inductive or capacitive manner depending upon voltage drop V_Lor V_C w.r.t current I.

From the phasor diagram:

Where

Z = Impedance of the circuit which offers opposition to current flow

Phase Angle

Again from the phasor diagram

Three cases of R-L-C Series Circuit

The equation for impedance is given as:

Case 1: When X_L>X_C

· The term (X_L-X_C) is positive.

· The circuit works as an R-L Series Circuit.

· Current lags behind voltage.

· Phase angle is positive.

· Power angle is positive.

· Power factor is lagging.

· Current flowing in circuit i,

Case 2: When X_C>X_L

· The term (X_L-X_C) is negative.

· The circuit works as an R-C Series Circuit.

· Current leads over voltage.

· Phase angle is negative.

· Power factor is negative.

· The current flowing in the circuit i,

Case 3: When X_L= X_C

· The term (X_L-X_C) = 0.

· The circuit works as pure resistance.

· Current is in phase with voltage.

· Phase angle is Zero.

· Power factor = 1.

· The current flowing in the circuit i,

6.4 True Power and Reactive Power

Table 6.1 Power in the electrical circuit

Formula

Units

1. True power

· Power consumed by watt meter

· Is the useful work and the current is in phase with the voltage

· Is the power consumed by resistance

· It is also known as active power

P_True= V×I Cosϕ

Watts

2. Reactive power

· Power consumed in L or C in a circuit is zero but the circulating power is termed as reactive power

· Does no useful work and current is 90^o out of phase with voltage.

· Reactive power cannot be measured by wattmeter.

P_Reac= V×I Sinϕ

VAR

3. Apparent power

· It is defined as the product of Voltage and Current

P_apparent= VI

6.5 Power Triangle

Figure 6.14 shows the power triangle for an A.C. circuit.

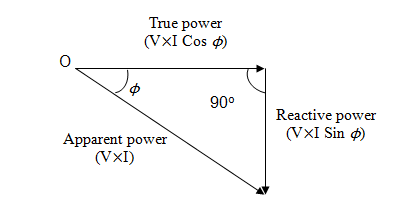
Fig. 6.14 Power triangle for an A.C. circuit

True power P_True= V×I Cos ϕ

Reactive Power P_Reac= V×I Sin ϕ

Apparent power P_app= VI

From power triangle

6.6 A.C. Parallel Circuits

In a.c. circuits R, L and C are connected in parallel. Voltage across each element is same but the current flowing through it is different. Equipments, lights and circuits are connected and operated in parallel. Parallel connection gives advantage that each equipment, appliance or device can be operated independently having separate switches for on/off. Parallel circuits are analysed using following methods:

1. Phasor diagram

2. Admittance method

3. Symbolic methods

Numerical

1. A coil of R = 100 ohm and L = 125 milli Henry is connected across alternating voltage e = 250 sin 100𝛑t. Determine:

a. Impedance

b. Current through the coil

Solution:

2πft = 100πt

f = 50 Hz

Inductive reactance X_L =