Module 2. A.C. series and parallel circuits
Lesson 9
STAR DELTA TRANSFORMATION
9.1 Transformations
Alternating voltage and current can be shown using phasor diagram. The problems can be analysed by using following two mathematical forms:
9.1.1 Rectangular form
Consider a voltage phasor V. The magnitude of the phasor is V and having θ angle from reference line OX.
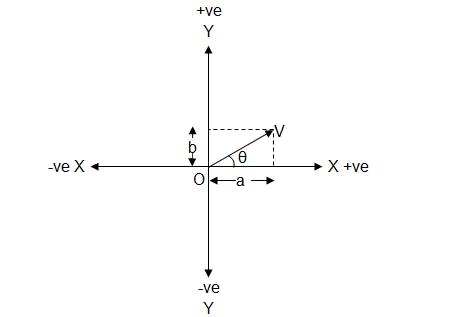
Fig. 9.1 Voltage phasor denoted by OV
Voltage phasor V = a + jb
Magnitude of phasor ![]()
![]()
9.1.2 Polar form
In polar form the phasor can be represented by the magnitude and the angle with the reference axis.
V = V∠ θ°
9.2 Conversion Methods
1. To convert Rectangular to polar form:
Rectangular form V = a + jb
![]()
![]()
Polar form = V ∠ θ°
2. To convert Polar to Rectangular form:
Rectangular form = V ∠ θ°
a = V cos θ
b = V sin θ
Polar form = a + jb
9.3 Numerical
Q.1 Convert 100 + j 50 to polar form:
Magnitude = ![]()
= 111.80
Phase angle = ![]()
= 26.56°
Polar form = 111.80∠ 26.56°
Q.2 Convert 100∠ 14.47° to rectangular form.
a = V cosθ
= 100 cos14.47°
= 96.82
b = V sin θ
=100 sin 14.47°
= 25
Rectangular form = 96.82 + j25
Q.3 Convert 200−j50 and −25−j20 into polar forms.
1. 200-j50 into polar
Magnitude = ![]()
= 206.15
Phase angle ![]()
![]()
= −14.03°
Polar form = 206.15∠−14.03°
2. −25−j20 into polar
Magnitude = ![]()
= 32.01
Phase
angle ![]()
= 38.65°
Polar form = 32.01∠38.65°
9.4 Adding and Subtraction of Phasors
The rectangular form is the simplest method for addition or subtraction of Phasors. If the phasors are represented in polar form, they should be first converted to rectangular form and then addition or subtraction be carried out.
(i) Addition: For the addition of phasors in the rectangular form, the real components are added together and the complex numbers (j components) are added together. Consider two voltage phasors:
V1 = a1 + jb1; V2 = a2 + jb2
Resultant Voltage V = V1 + V2 = (a1 + jb1) + (a2 + jb2)
= (a1 + a2) + j(b1 + b2)
Magnitude of resultant, V ![]()
Angle from OX-axis, ![]()
(ii)Subtraction is done similar to what was done in phasor addition
V = V1 −V2 = (a1 + jb1) − (a2 + jb2)
= (a1 − a2) + j(b1 − b2)
Magnitude of resultant
voltage,
![]()
Angle from
OX-axis, ![]()
9.5 Multiplication and Division of Phasors
Multiplication and division of phasor is done in polar form as the method is simpler compared to what is done in rectangular form. Consider two phasor:
V1 = a1 + jb1 = V1∠θ1
V2 = a2 + jb2 = V2∠θ2
9.5.1 Multiplication
(i) Rectangular form,
V1 × V2 = (a1 + jb1) (a2 + jb2)
= a1a2 + ja1b2 + ja2b1 + j2b1b2
= (a1a2−b1b2) + j(a1b2 + a2b1) (as j2=−1)
Magnitude of resultant ![]()
Angle w.r.t. OX-axis, ![]()
(ii) Polar form. To multiply the phasors that are in polar form, multiply their magnitudes and add the angles (algebraically).
V1 × V2 = V1∠θ1× V2 ∠θ2 = V1V2∠ θ1+ θ2
Multiplication of phasors becomes easier when they are expressed in polar form.
9.5.2 Division
(i) Rectangular
form,
![]()
![]()
![]()
![]()
(ii) Polar Form. To divide the phasors that are in polar form, the magnitude of phasors are divided and denominator angle is subtracted from the numerator angle.
![]()
9.6 Transformation
9.6.1 Star to delta (Y/∆) transformation
In any electrical system a star Y connection may be replaced by an equivalent ∆-connected system. A 3-phase star system having voltage VL and line current IL may be replaced by a ∆-connected system having phase voltage VL and phase current IL/√3. Y-connected load having branch impedances each of Z∠∅ may be replaced by an equivalent ∆-connected load having phase impedance is 3Z∠∅ (Fig. 1.2).
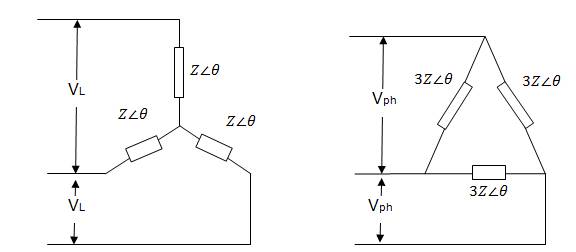
Fig. 9.2 Star to delta (Y/∆) transformation
For a balanced star-connected load, let
VL = line voltage;
IL = line current;
Z∠∅ = impedance per phase
Then for an equivalent ∆-connected system,
Phase voltage Vph = VL
Phase current Iph = IL / √3
Zph = 3Z∠∅
ZY = VL / (√3 IL)
9.6.2 Delta to star (∆/Y) transformation
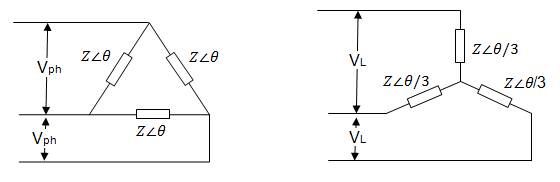
Fig. 9.3 Delta to star (∆/Y) transformation
Now, in the equivalent ∆-connected systems, the line voltages and currents must have the same values as in the Y-connected system, hence we must have
VL= Vph
Iph = IL / √3
Z∆ = VL / (IL / √3) = √3 VL/ IL = 3ZY
Z∆ ∠ ∅ = 3 ZY∠ ∅ (∵VL/ IL = 3ZY)
Z∆ = 3 ZY or ZY = Z∆ /3
Numerical
1. A 220 V 3 phase Y connected load is shown in following diagram. The phase sequence is RYB. Calculate the line currents and neutral line current.
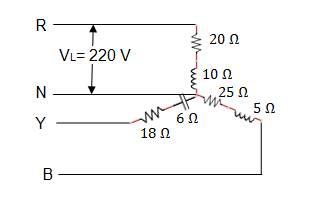
ZR = (20 + j10) = 22.36∠26.56o
ZY = (18 + j6) = 18.97∠18.43o
ZY = (25 + j5) = 25.49∠11.30o
Let
line voltages with difference of phase angle 120o
VRN = 220∠0o
VYN = 220∠─120o
VBN = 220∠─240o
Line currents:
IR
= VRN/ZR = ![]() =9.83∠─26.56o = 8.79 ─ j4.39 A
=9.83∠─26.56o = 8.79 ─ j4.39 A
IY
= VYN/ZY = ![]() =11.59∠─138.43o = ─ 8.67 ─ j7.69 A
=11.59∠─138.43o = ─ 8.67 ─ j7.69 A
IB
= VBN/ZB = ![]() =8.63∠─251.3o = ─ 2.76 + j8.17 A
=8.63∠─251.3o = ─ 2.76 + j8.17 A
IN = IR + IY + IB
= 8.79 ─ j4.39 ─ 8.67 ─ j7.69 ─ 2.76 + j8.17
IN = ─ 2.64 + j4.87 = 5.53∠118.46o A
2. Consider 75 ohm resistors are connected in star and then in delta. If line voltage VL = 440 V calculate line and phase current in star and delta system.
Solution
Star connection
Phase voltage Vph = VL/√3 = 440/√3 = 254.03 V
Phase current Iph = Vph / Z ph = 254.03/75 = 3.38 A
Line current IL = Phase current Iph = 3.38 A
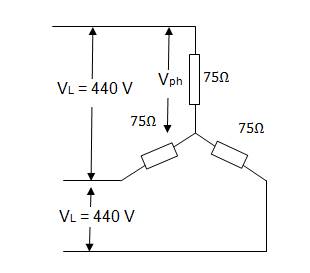
Delta connection
Phase voltage Vph = Line voltage VL = 440 V
Phase current Iph = Vph / Zph = 440/75 = 5.86 A
Line current IL = Iph
X √3 = 5.86 X √3 = 10.14 A