Module 9. Dimensional analysis
Lesson 26
BUCKINGHAM’S THEOREM APPLICATION TO FLUID FLOW PHENOMENA
26.1 Dimensions
In the SI system there are seven fundamental units: kilogram, meter, candela, second, ampere, kelvin, and mole. These are also known as fundamental quantities. In fluid mechanics mostly kg, m, s and K is used. Quantities like force, pressure, energy, acceleration etc are expressed in combination of fundamental quantities and are therefore called derived quantities. Few of them are mentioned in Table 26.1.
Table
26.1 Quantities, dimensions, and units
|
Quantity |
Dimensions (M LT) |
Preferred units (SI) |
|
Length (L) |
L |
m |
|
Time (T) |
T |
s |
|
Mass (M) |
M |
kg |
|
Area (A) |
L2 |
m2 |
|
Volume (Vol) |
L3 |
m3 |
|
Velocity (V) |
LT-1 |
m/s |
|
Acceleration (a) |
LT-2 |
m/s2 |
|
Discharge (Q) |
L3 T-1 |
m3/s |
|
Force (F) |
MLT-2 |
N |
|
Pressure (p) |
ML-1T‑2 |
Pa |
|
Shear stress (τ) |
ML-1T‑2 |
N/m2 |
|
Density (ρ) |
ML-3 |
kg/m3 |
|
Specific weight (ω) |
ML-2T-2 |
N/m3 |
|
Energy/Work/Heat (E) |
ML2T-2 |
J |
|
Power (P) |
ML2T-3 |
W |
|
Dynamic viscosity (μ) |
ML-1T1 |
N s/m2 or Pa.s |
|
Kinematic viscosity (υ) |
L2 T-1 |
m2/s |
26.2 Dimensional Analysis
The principal use of dimensional analysis is to deduce from a study of the dimensions of the variables in any physical system certain limitations on the form of any possible relationship between those variables. The method is of great generality and mathematical simplicity. Dimensional Analysis is a process of arranging various factors is arranged in a manner that it forms dimensionless number.
26.3 Dimensional Homogeneity
An equation will be dimensionally homogeneous if the dimensions of various terms on the two sides of the equation are identical. A dimensionally homogeneous equation is independent of the fundamental units of measurement and is applicable to all systems of units For e.g. taking the following equation:
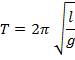
Dimension
of
L.H.S
[T]
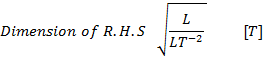
The dimension of L.H.S is same as that of R.H.S. = [T]. Thus the equation may be said to be dimensionally homogeneous.
Other examples of dimensional homogeneity:
· ![]()
· Q=VA
· ![]()
26.4 Application of Dimensional Analysis
· The first step to dimensional analysis is to determine the dimensional homogeneity of any equation.
· Analysis helps to determine the dimensions and thus the units of any quantity.
· Units can be easily transformed from one system to another.
· To establish relationship between number of variables.
· To reduce equations by arranging variables in dimensionless forms.
26.5 Steps for Dimensional Analysis
The application of dimensional analysis to mathematically represent engineering problems consists of several steps. These are:
(1) formulate a differential equations and/or algebraic expressions which adequately describe the problem, together with the required boundary conditions;
(2) select the appropriate dimensionless variables tor all independent and dependent variables involved, using arbitrary terms or boundary values for the denominator in each case;
(3) substitute the new dimensionless variables into each differential equation and boundary condition to normalize them;
(4) group into functional form all dimensionless variables and those parameters generated;
(5) reduce the functionality to the minimum possible number of independent groups; and
(6) drop any groups in which the arbitrary terms can not be divided out using other groups of the functionality.
26.6 Rayleigh’s Method for Dimensional Analysis
Rayleigh’s method for dimensional analysis involves following steps:
· Independent variables are identified which will express the functional relationship most closely. A maximum of three to four variables must be selected.
· If the dependent variable X is some function of the independent variables x1, x2, x3….,the equation can be given as:
![]()
Above equation may be written as:
![]()
Here C is a dimensionless coefficient to be determined through experiments
Values of a, b, c etc are determined by comparing the powers on both sides.
26.7 Buckingham’s π- method
It states
that if there are ‘n’ variables in a dimensionally homogeneous equation and if these
variables contain ‘m’ fundamental (primary) dimensions then the variables can
be grouped into (n-m) dimensionless terms. These dimensionless terms are called
![]() terms.
terms.
We use M L T fundamental quantities in fluid mechanics.
Mathematically if x1 depends on other variables x2, x3, x4...xn the equation can be given as
x1 = f ( x2, x3, x4 ……………, xn)
f(x1, x2, x3, x4 ……………, xn) = 0 .........(i)
Where x are dimensional physical quantities such as velocity, density, pressure, area, diameter etc. Then the phenomenon given in equation (i) can be described by (n-m) dimensionless ‘π’ terms.
f (π1, π2,…………………. π n-m)
where ‘m’ represents the fundamental dimensions such as mass, length and time.
26.8 Numerical
Q 1. The resistance R experienced by a partially submerged body depends upon the velocity V, length of the body l, viscosity of the fluid µ, density of the fluid ρ and gravitational acceleration g. Obtain a dimensionless express for R.
Solution:
Mathematically following relation can be given:
![]()
![]()
Number of variable n = 6
Number of fundamental variable m = 3
Therefore, number of π-terms = n-m = 6-3 = 3 π-terms
Choosing length l, velocity V, and density ρ as the 3 repeating variables.
Analysis of π-terms.
a.
![]()
![]()
Equating powers of M, L and T on both sides
![]()
![]()
![]()
![]()
b.
![]()
![]()
Equating powers of M, L and T on both sides
![]()
![]()
![]()
![]()
c.
![]()
![]()
Equating powers of M, L and T on both sides
![]()
![]()
![]()
![]()
The functional relationship can be given as:
![]()
![]()
![]()
![]()
Since reciprocal of π-term and its square root is non-dimensional.
![]()
It is
evident that resistance R is a function of Reynolds number (![]() ) and Froude’s number (
) and Froude’s number (![]() ).
).