Fluid Mechanics 3(2+1)

LESSON 3. PROPERTIES OF FLUID

3.1.2 Density of a fluid (r)

Definition:  mass per unit volume,

slightly affected by changes in temperature and pressure. 

                                                = mass/volume  = m/v                 

            Units: kg/m³

            Typical values:          

            Water = 1000 kg/m3;   Air = 1.23 kg/m3

• Viscosity, m, is a measure of resistance to fluid flow as a result of intermolecular cohesion. In other words, viscosity can be seen as internal friction to fluid motion which can then lead to energy loss.

• Different fluids deform at different rates under the same shear stress. The ease with which a fluid pours is an indication of its viscosity. Fluid with a high viscosity such as syrup deforms more slowly than fluid with a low viscosity such as water. The viscosity is also known as dynamic viscosity.

• Units:  N.s/m² or kg/m/s

• Typical values:                   

Water = 1.14x10^-3 kg/m/s;   

Air      = 1.78x10^-5 kg/m/s 

3.1.3 Viscosity (m)

• Viscosity, m, is a measure of resistance to fluid flow as a result of intermolecular cohesion. In other words, viscosity can be seen as internal friction to fluid motion which can then lead to energy loss.

• Different fluids deform at different rates under the same shear stress. The ease with which a fluid pours is an indication of its viscosity. Fluid with a high viscosity such as syrup deforms more slowly than fluid with a low viscosity such as water. The viscosity is also known as dynamic viscosity. 

• Units:  N.s/m2 or kg/m/s

• Typical values:                                                            

Water = 1.14x10-3 kg/m/s;  

 Air = 1.78x10-5 kg/m/s

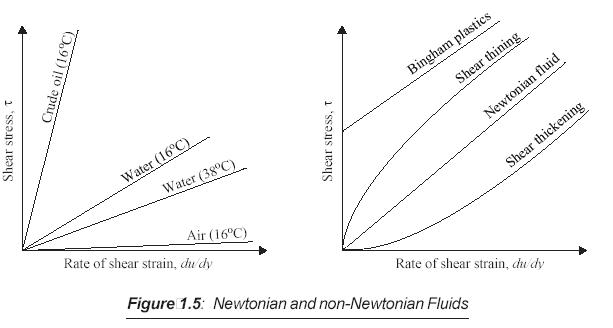
 3.1.4 Newtonian and Non-Newtonian Fluid

Newton’s’ law of viscosity is given by;

\[\tau=\mu{{du}\over{dy}}\]

t   = shear stress

m  = viscosity of fluid

du/dy = shear rate, rate of strain or velocity gradient

• The viscosity m is a function only of the condition of the fluid, particularly its temperature.

• The magnitude of the velocity gradient (du/dy) has no effect on the magnitude of m.

• The viscosity of the non-Newtonian fluid is dependent on the velocity gradient as well as the condition of the fluid.

Newtonian Fluids

• a linear relationship between shear stress and the velocity gradient (rate of shear),

• the slope is constant

• the viscosity is constant

 Non-Newtonian Fluids

slope of the curves for non-Newtonian fluids varies

 

 

 

 

 

 

 

 

 

If the gradient m is constant, the fluid is termed as Newtonian fluid.  Otherwise, it is known as non-Newtonian fluid.  Fig. 1.5 shows several Newtonian and non-Newtonian fluids.

3.1.5 Kinematic viscosity, n

 Definition: is the ratio of the viscosity to the density;

\[\nu=\mu /\rho\]

• will be found to be important in cases in which significant viscous and gravitational forces exist.

                Units: m²/s

                Typical values:            

                Water = 1.14x10-6 m2/s;            Air = 1.46x10-5 m2/s;    

In general,

• viscosity of liquids decrease  with  increase in temperature, whereas

• viscosity of gases  increases with increase  in temperature.

 3.1.6 Specific Weight

   Specific weight of a fluid, g

• Definition: weight of the fluid per unit volume

• Arising from the existence of a gravitational force  

• The relationship g and g can be found using the following:

                Since                     ρ =  m/v             

                therefore              Υ= ρg                  

• Units: N/m³
• Typical values:            

                                Water = 9814 N/m³;    

                                Air = 12.07 N/m³

3.1.7 Specific Gravity

The specific gravity (or relative density) can be defined in two ways:

Definition 1: A ratio of the density of a liquid to the density of  water at standard temperature and pressure (STP) (20°C, 1 atm),      or

Definition 2: A ratio of the specific weight of a liquid to the specific weight of water  at standard temperature and pressure (STP) (20°C, 1 atm),  

\[SG={{\rho_{liquid}}\over{\rho_{water@STP}}}={{\gamma_{liquid}}\over{\gamma _{water@STP}}}\]

• Unit: dimensionless.

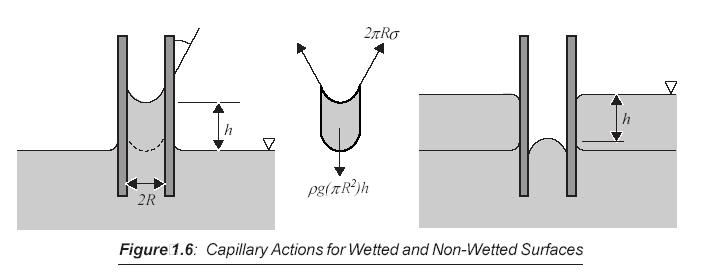
3.1.8 Surface Tension

• Surface tension coefficient s can be defined as the intensity of intermolecular traction per unit length along the free surface of a fluid, and its SI unit is N/m.

• The surface tension effect is caused by unbalanced cohesion forces at fluid surfaces which produce a downward resultant force which can physically seen as a membrane.

• The coefficient is inversely proportional to temperature and is also dependent on the type of the solid interface. 

• For example, a drop of water on a glass surface will have a different coefficient from the similar amount of water on a wood surface.

• The effect may be becoming significant for small fluid system such as liquid level in a capillary, as depicted in following figure, where it will decide whether the interaction form by the fluid and the solid surface is wetted or non-wetted.

• If the adhesion of fluid molecules to the adjacent solid surface is stronger than the intermolecular cohesion, the fluid is said to wet on the surface. Otherwise, it is a non-wetted interaction.
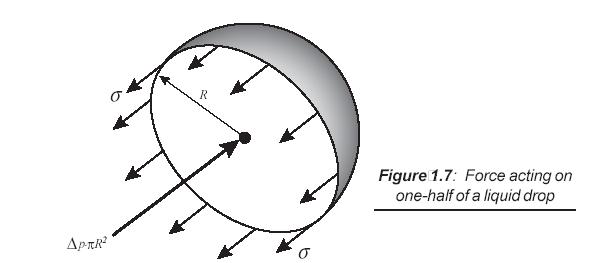
• The pressure inside a drop of fluid can be calculated using a free-body diagram of a spherical shape of radius R cut in half, as shown in following figure, and the force developed around the edge of the cut sphere is 2pRs.

• This force must be balance with the difference between the internal pressure p_i and the external pressure p_e acting on the circular area of the cut.  Thus,

2Rσ = ΔppR²

\[\Delta p{\rm{ }}={\rm{ }}p_{\rm{i}} -p_{\rm{e}} {\rm{ }} = {\rm{ }}{{2\sigma } \over R}\]

3.1.9 Vapour Pressure and cavitation

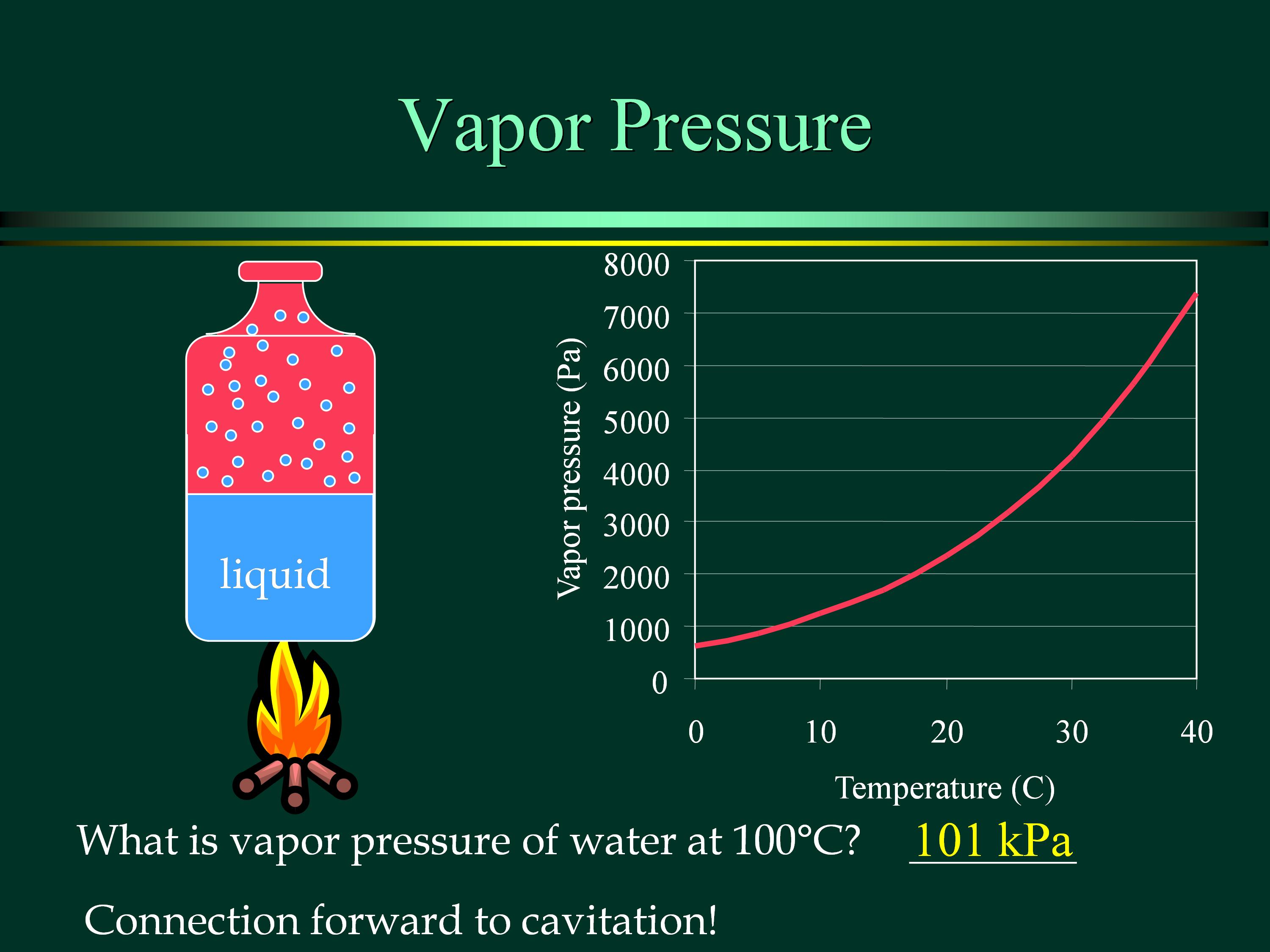
Vapour pressure is the partial pressure produced by fluid vapour in an open or a closed container, which reaches its saturated condition or the transfer of fluid molecules is at equilibrium along its free surface.

In a closed container, the vapour pressure is solely dependent on temperature.  In a saturated condition, any further reduction in temperature or atmospheric pressure below its dew point will lead to the formation of water droplets.

On the other hand, boiling occurs when the absolute fluid pressure is reduced until it is lower than the vapour pressure of the fluid at that temperature.

For a network of pipes, the pressure at a point can be lower than the vapour pressure, for example, at the suction section of a pump.  Otherwise, vapour bubbles will start to form and this phenomenon is termed as cavitation.

In short:

• Vapor Pressure P_v is defined as the pressure exerted by its vapor in phase equilibrium with its liquid at a given temperature

• If P drops below P_v, liquid is locally vaporized, creating cavities of vapor. 

• Vapor cavities collapse when local P rises above P_v.

• Collapse of cavities is a violent process which can damage machinery.

Cavitation is noisy, and can cause structural vibrations

3.2 REAL and ideal fluids

(1) Ideal fluid – no friction, fluid can ‘slide’ tangentially along the solid boundary.
(2) Real fluid – will possess friction (or viscosity), fluid cannot ‘slide’ along boundary – no slip boundary condition.Tangential velocity = zero if the wall is at rest.
(3) Velocity component perpendicular to the wall must be the same as that of the wall – no penetration condition (= zero if the wall is at rest).

An ideal fluid is assumed

• to be incompressible (so that its density does not change),

• to flow at a steady rate,

• to be nonviscous (no friction between the fluid and the container through which it is flowing), and

• flows irrotationally (no swirls or eddies).

• In a real fluid viscosity produces resistance to motion  by causing shear or friction forces between fluid particles and between these and boundary walls. 

• Due to this viscous effects, fluid tends to ‘stick’ to solid surfaces and have stresses within their body.

• The inclusion of viscosity allows the existence of two physically distinct flow regimes, known as laminar and turbulent flow.