Fluid Mechanics 3(2+1)

LESSON 4. PRESSURE

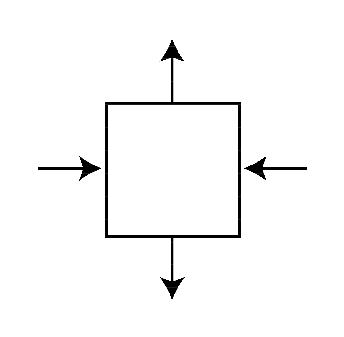
p = 0

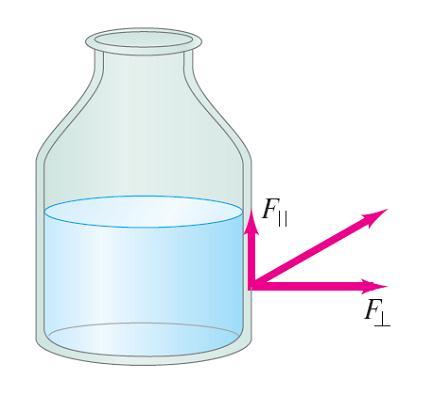
• The basic property of a static fluid is pressure.
• Pressure is defined as the amount of surface force exerted by a fluid on any boundary it is in contact with. It can be written as:

\[Pressure={{Force}\over{Area\;of\;which\;the\;force\;is\;applied}}\]
\[P={F\over A}\quad \]

Unit: N / m² or Pascal (Pa).

(Also frequently used is bar, where 1 bar = 10⁵ Pa).

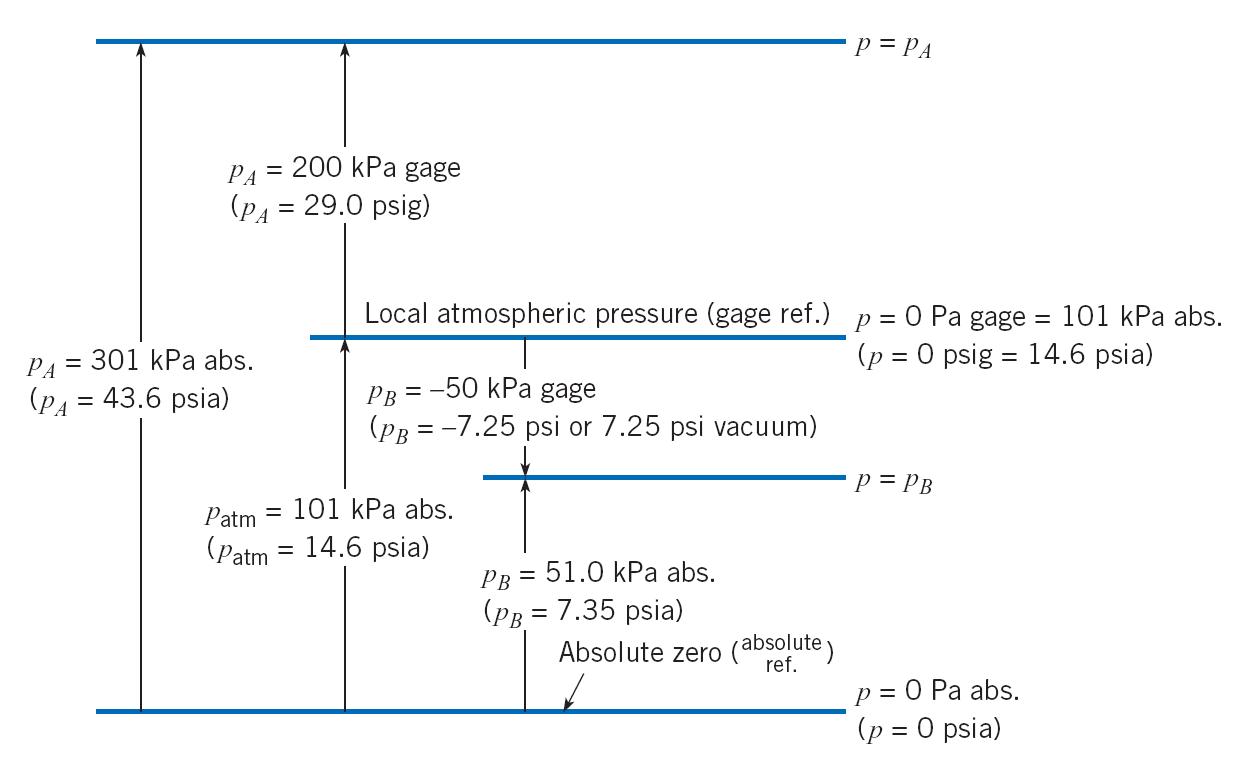
4.2 Absolute Pressure, Gage Pressure, and Vacuum

• Pressure in a vacuum is  p = 0.

• Absolute pressure is referenced to perfect vacuum.

•  Gage pressure is referenced to another pressure, typically atmospheric pressure (most gages measure relative pressures).

• Pressure measurements are generally indicated as being either absolute or gauge pressure.

• is the pressure measured above or below the atmospheric pressure (i.e. taking the atmospheric as datum). 

• can be positive or negative. 

• A negative gauge pressure is also known as vacuum pressure. 

• uses absolute zero, which is the lowest possible pressure.

• Therefore, an absolute pressure will always be positive.

• refers to the prevailing pressure in the air around us.

• It varies somewhat with changing weather conditions, and it decreases with increasing altitude. 

• At sea level, average atmospheric pressure is 101.3 kPa (abs), 14.7 psi (abs), or 1 atmosphere (1 bar = 1x10⁵ Pa). 

• This is commonly referred to as ‘standard atmospheric pressure’.

• A simple equation relating the two pressure measuring system can be written as

4.2.1 Gauge pressure

• is the pressure measured above or below the atmospheric pressure (i.e. taking the atmospheric as datum). 

• can be positive or negative. 

• A negative gauge pressure is also known as vacuum pressure. 

4.2.2 Absolute pressure

• uses absolute zero, which is the lowest possible pressure.

• Therefore, an absolute pressure will always be positive.

4.2.3 Atmospheric pressure                         

• refers to the prevailing pressure in the air around us.

• It varies somewhat with changing weather conditions, and it decreases with increasing altitude. 

• At sea level, average atmospheric pressure is 101.3 kPa (abs), 14.7 psi (abs), or 1 atmosphere (1 bar = 1x10⁵ Pa). 

• This is commonly referred to as ‘standard atmospheric pressure’.

• A simple equation relating the two pressure measuring system can be written as:

                               P_abs = P_gauge + P_atm           

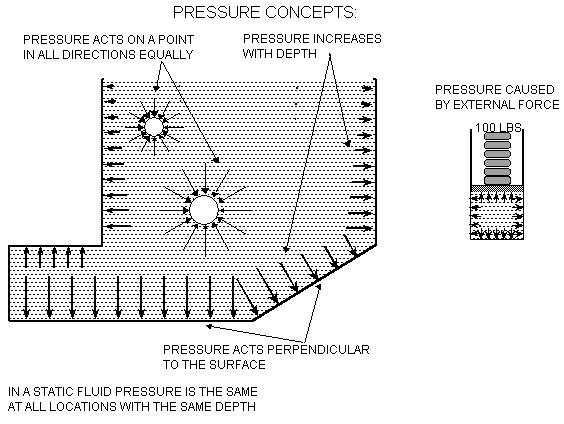
• Pressure acts uniformly in all directions on a small volume of fluid.

• In a fluid confined by solid boundaries, pressure acts perpendicular to the boundary.

• These principles, called Pascal’s Law,

• A fluid at rest exerts pressure perpendicular to any surface that it contacts. There is no parallel component that would cause a fluid at rest to flow.

 

 

 

4.3  Variations of Pressure with Elevation

• To find the variations of pressure with elevation, let’s consider a small cylindrical element of fluid of cross-sectional area A, and height (h = Z₂ –Z₁), surrounded by the same fluid of mass density, r.

• The pressure at the bottom of the cylinder is P₁ at level Z₁, and at the top is P₂ at level Z₂. The fluid is at rest and in equilibrium so all the forces in the vertical direction sum to zero.

• Force due to P₁ (upward) = P₁A

• Force due to P₂ (downward) = P₂A

• Force due to weight of element = mg = ρgA(Z₂-Z₁)

• Taking the summation of forces (upward as positive);

                                                                   (↑­)ΣF=0

                                                                   P₁A – P₂A - ρgA(Z₂-Z₁) = 0

                                                                   P₁ – P₂ = ρg (Z₂-Z₁) = ρgh                          

                                                     or           P₂ – P₁ = - ρg(Z₂-Z₁) = - ρgh                      

Thus, in any fluid under gravity,

• an increase in elevation causes a decrease in pressure. 

• a decrease in elevation causes an increase in pressure.