Site pages
Current course
Participants
General
MODULE 1. FLUIDS MECHANICS
MODULE 2. PROPERTIES OF FLUIDS
MODULE 3. PRESSURE AND ITS MEASUREMENT
MODULE 4. PASCAL’S LAW
MODULE 5. PRESSURE FORCES ON PLANE AND CURVED SUR...
MODULE 6.
MODULE 7. BUOYANCY, METACENTRE AND METACENTRIC HEI...
MODULE 8. KINEMATICS OF FLUID FLOW
MODULE 9: CIRCULATION AND VORTICITY
MODULE 10.
MODULE 11.
MODULE 12, 13. FLUID DYNAMICS
MODULE 14.
MODULE 15. LAMINAR AND TURBULENT FLOW IN PIPES
MODULE 16. GENERAL EQUATION FOR HEAD LOSS-DARCY EQ...
MODULE 17.
MODULE 18. MAJOR AND MINOR HYDRAULIC LOSSES THROUG...
MODULE 19.
MODULE 20.
MODULE 21. DIMENSIONAL ANALYSIS AND SIMILITUDE
MODULE 22. INTRODUCTION TO FLUID MACHINERY
LESSON 6. PASCAL’S LAW
Pascal’s Principle
if an external pressure is applied to a confined fluid, the pressure at every point within the fluid increases by that amount. Applications: hydraulic lift and brakes
Pascal’s law
-
Pressure acts uniformly in all directions on a small volume of fluid.
-
In a fluid confined by solid boundaries, pressure acts perpendicular to the boundary.
-
These principles, called Pascal’s Law,
Application of Pascal’s law
1. A Hydraulic Jack Lifting a Car
The back end (half the weight) of a car of mass 2000 kg is lifted by an hydraulic jack where the As / Al ratio is 0.1 (the area of the large cylinder is 10 times the area of the small cylinder).
The force (weight) acting on the large cylinder can be calculated with Newton's Second Law:
Fl = m a
where
m = mass (kg)
a = accelaration of gravity (m/s2)
or
Fl = 1/2 2000 (kg) 9.81 (m/s2)
= 9810 (N)
The force acting on the small cylinder can be calculated with (2d)
Fs = 9810 (N) 0.1
= 981 (N)
2. The siphon
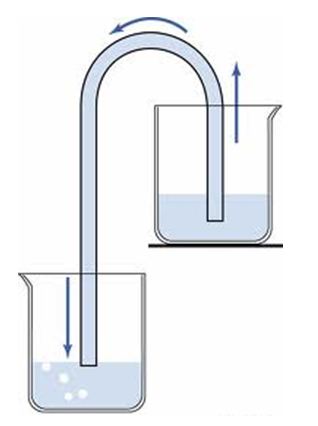
A siphon works because gravity pulling down on the taller column of liquid causes reduced pressure at the top of the siphon
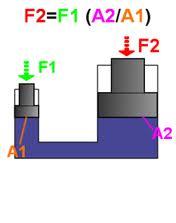
3. The underlying principle of the hydraulic jack and hydraulic press
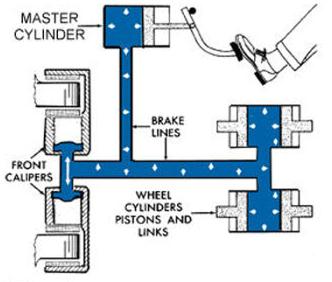
4. Force amplification in the braking system of most motor vehicles.
5. Used in artesian wells, water towers, and dams.
6. At a depth of 10 meters under water, pressure is twice the atmospheric pressure at sea level, and increases by about 100 kPa for each increase of 10 m depth.
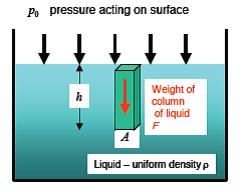
In a static fluid, with uniform density ρ,
Pressure at depth, h = pressure acting on surface + pressure due to height of liquid
Ph = P0 + F/A
F = weight of column liquid of cross sectional area A
F = mg
M = ρV = ρAh
F/A = ρgh
Ph = P0 + ρgh
Last modified: Monday, 16 September 2013, 6:40 AM