Fluid Mechanics 3(2+1)

LESSON 7. PRESSURE FORCES ON PLANE SURFACES

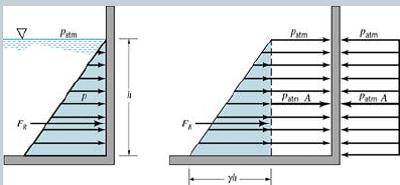
• For horizontal plane submerged in a liquid, the pressure, P, will be equal at all points of the surface. This leads to the conclusion that the resultant force on horizontal surface due to that pressure can be computed from the simple product of pressure times the area of interest, i.e.

                        Force = Pressure x Area of plane

                        F = PA 

                       This force will act vertically downward and through the center of pressure

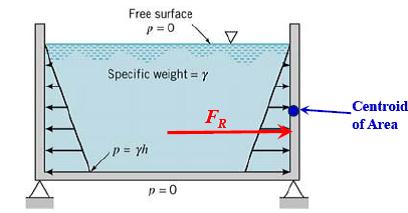
Hydrostatic Force on a Vertical Plane Surface

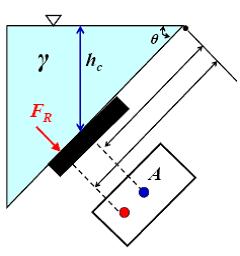
Hydrostatic Pressure on an Inclined Surface

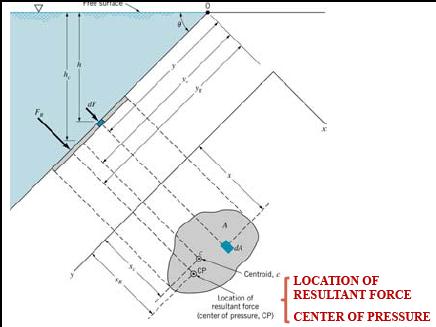
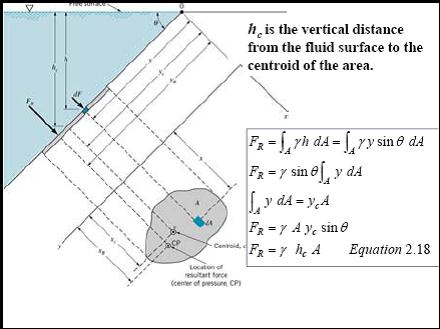
Resultant Force and Center of Pressure on a Submerged Plane Surface in a Liquid

• below shows a plane surface PQ of an area A submerged in a liquid of density, r, and inclined at an angle f to the free surface.

• Considering one side only, there will be a force due to fluid pressure, acting on each element of area dA, the magnitude of the pressure will depend on the vertical depth y of the element below the free surface. Taking the pressure at the free surface as zero, the pressure at a distance y below the free surface can be written as:

                        p = ρgy.          

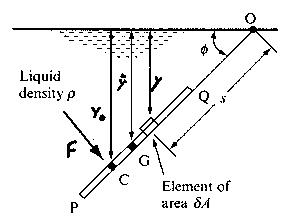
Figure 1. Resultant force on a plane surface immersed in a fluid

• Force on elemental area δA:  

dF = PδA = ρgyδA                  (1)

• The resultant force acting on the plane can be found by summing all the forces on the small element:

                        F = ΣPδA =  Σρgy δA               (2)

• Assuming that r and g are constant,

                        F = ρg Σy δA                            (3)

• The quantity Σy δA is the first moment of area under the surface PQ about the free surface of the liquid and is equal to Aŷ, where A = the area of the whole immersed surface and ŷ = vertical distance from the free surface to the centroid of the area, G, of the immersed surface.

• Centroid of the area is defined as the point at which the area would be balanced if suspended from that point. It is equivalent to the center or gravity of a solid body.

• Substituting into equation (2) will give

                        F =ρgŷA                                  (4)

• It may be noted that the resultant force, F, is independent of the angle of inclination f so long as the depth of the centroid ŷ is unchanged.

• The point of application of the resultant force on the submerged area is called the center of pressure. This resultant force will act perpendicular to the immersed surface at the center of pressure, C.

• The vertical depth of the center of pressure, y₀,  below the free surface can be found using the following:

                              \[y_o=\hat y+{{I_g }\over{A\hat y}}\]               ...(5)

• where

                        Ig = second moment of plane area about its center of gravity

                        A = the area of the whole immersed surface

                        ŷ = vertical distance from the free surface to the centroid of the area A

• The above equation implies that the center of pressure is always below the centroid.