Fluid Mechanics 3(2+1)

LESSON 10. BUOYANCY

It is used by architects and engineers when they design ships, submarines and various other floating structures.

1. The buoyant force exerted on a submerged or floating body is equal to the weight of the fluid displaced by the body.

2. A floating body displaces a weight of fluid equal to its own weight; i.e., a floating body is in equilibrium.

The center of buoyancy is located at the centroid of the displaced fluid volume.

In the case of a body lying at the interface of two immiscible fluids, the buoyant force equals the sum of the weights of the fluids displaced by the body.

• When a body is submerged or floating in a static fluid, the resultant force  exerted on it by the fluid is called the buoyancy force. This buoyancy force is always acting vertically upward, and has the following characteristics;

• The buoyancy force is equal to the weight of the fluid displaced by the solid body.

• The buoyancy force acts through the centroid of the displaced volume of fluid, called the center of buoyancy.

• A floating body displaces a volume of fluid whose weight is equal to the weight of the body

• The above  principle is known Archimedes’ principle and can be defined mathematically as demonstrated below ;

• The buoyancy of a body wholly or partly immersed in a fluid at rest , situated in a gravitational field or other field of force is defined as the upward thrust of the fluid on the body. Generally all problems relating to buoyancy can be resolved by applying the principles of Archimedes.

In short

“The buoyancy of any body is vectorially equal and opposite to the weight of the fluid displaced by the body and has the same line of action”.

• The upward thrust which the surrounding fluid exerts on an object is referred to as the force of buoyancy.

• This thrust acts through the centroid of the displaced volume, referred to as the centre of buoyancy.

• The centre of buoyancy is not the same as the centre of gravity which relates to the distribution of weight within the object.

• If the object is a solid with a uniform density exactly the same as water and the body is immersed in water the force of buoyancy will be exactly equal to the weight and the centre of buoyancy will be the same as the centre of gravity.

• The object will be in equilibrium with the surrounding fluid.

• This principle also applied to gases as well as liquids and explains why balloons filled with gases which have lower density compared to air rise to such a height that the weight of the air displaced is equal to the weight of the gas in the balloon.

• A body which hovers in a fluid and is in equilibrium is said to have neutral buoyancy.

If the centre of gravity (G) is not in the same location as the centroid (centre of buoyancy-B). The body will orient itself such that the centre of Gravity is below the centre of buoyancy. (See diagram below). The diagram below shows a hollow vessel with a heavy weight occupying a small segment. The diagram below shows the object in a fully stable equilibrium position. In theory if the G was vertically above B then there is no force (moment) tending to rotate the object and it is still in a position of equilibrium. In this position however it is considered to be unstable.

Metacentre and Metacentric Height

Consider a rectangular vessel immersed as shown below in the first figure the centre of buoyancy at B and the centre of gravity is at G. with the water line at S-S Now if the vessel is heeled such that the water line is at S'=S'. The centre of buoyancy now moves to B' as shown in the second figure below. There is now an upthrust (W) due to buoyancy at B' and the weight of the vessel (W) is acting down at G and there is a couple W.a acting to restore the vessel to its original position. The locus of each position of B' as the vessel heels to different angles is called the buoyancy curve. Also the curve joining the tangents of each line of thrust, drawn relative to the vessel, is known as the curve of metacentres. The cusp of this curve is known as the initial metacentre. This is shown on the third figure which combines the first and second figures

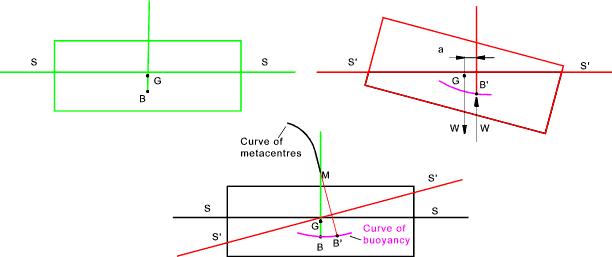
The initial metacentre M is the point where the line of action of the upthrust intesects the original vertical line through the centre of buoyancy B and the centre of gravity G for an infinitesimal angle of heel.
The righting moment is calculated as W.GM.sinθ. The angle of heel being θ. For small values of heel up to about 15^o GM is fairly constant and is the value generally accepted as the traverse metacentric height of the vessel
A floating vessel is stable if the metacentre lies above the centre of gravity G.
A floating vessel is in neutral equilibrium if the metacentre lies on the centre of gravity G.
A floating vessel is unstable if the metacentre lies below the centre of gravity G.

Centre of Pressure on Submerged surfaces

The point at which the resultant fluid force is considered to act on a plane area is called its centre of pressure. This is shown on the above figure at point P. This point is found by summing the moments of the elementary forces about the imaginary axis. O - O'.

M = ∑ δ M = ∑ p x δ A = ρ g sin θ ∑ x ² δ A

This is equivalent to the moment exerted by the resultant force F acting through the centre of pressure P. Thus

M = F x_P = [ρg sin θ ∑ x δA] x _P

 And from above the force (F) on the plate is

F = ρg sin θ ∑ x .δA

Therefore,

The second moment of area of the plane figure about its centroid G is I_G
The first moment of area of a plane figure about O-O= A.x_G.
Using the parallel axis theorem I_O = I_G + A. x_G².
This can be expressed in terms of radii of gyration as A k_o² = A [k_G² + x_G²] Therefore

Therefore the centre of pressure of a plane area lies below the centroid G of the area by a distance P - G = x _P - x _G = k _G² / x _G measured along the slope of the plane. As the radius of gyration of the surface about it's centroid k_G is fixed the difference reduces as the depth of the surface increases.

Theory

Floating bodies are a special case; only a portion of the body is submerged, with the remainder poking of the free surface. The buoyancy, Fa, which is the weight of the displaced water, i.e., submerged body portion, is equal to its dead weight, FG. The centre of gravity of the displaced water mass is referred to as the centre of buoyancy, A and the centre of gravity of the body is known as the centre of mass, S.

In Equilibrium position buoyancy force, FA, and dead weight, FG, have the same line of action and are equal and opposite (see Fig. 2). A submerged body is stable if its center of mass locates below the center of buoyancy. However, this is not the essential condition for stability in floating objects

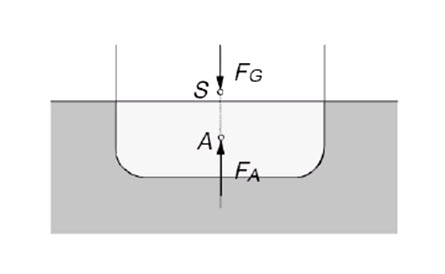
Figure 2- Buoyancy force and center of buoyancy

A floating object is stable as far as a resetting moment exists in the event of deflection or tilting from the equilibrium position. As shown in Fig. 3, dead weight FG and buoyancy FAform a force couple with the lever arm of B, which provides a righting moment. The distance between the centre of gravity and the point of intersection of line of action of buoyancy and symmetry axis, is a measure of stability. The point of intersection is referred to as the metacentre, M, and the distance between the centre of gravity and the metacentre is called the metacentric height ZM.

The floating object is stable when the metacentric height Zm is positive, i.e., the metacenter is located above the centre of gravity; else it is unstable.

The position of the metacenter is not governed by the position of the centre of gravity. It merely depends on the shape of the portion of the body under water. There are two methods of determining the metacenter position.

In the first method, the centre of gravity is laterally shifted by a certain constant distance, Xs, using an additional weight, causing the body to tilt. Further vertical shifting of the centre of gravity alters the heel angle a. A stability gradient formed from the derivation dxs/da is then defined which decreases as the vertical centre of gravity position approaches the metacentre. If centre of gravity position and metacentre coincide, the stability gradient is equal to zero and the system is stable. This problem is easily solved graphically (see Fig. 4). The vertical centre of gravity position is plotted versus the stability gradient. A curve is drawn through the measured points and extrapolated as far as it contacts the vertical axis. The point of intersection with the vertical axis locates the position of the metacentre.

The metacentric height can also be evaluated theoretically using the following relationship:

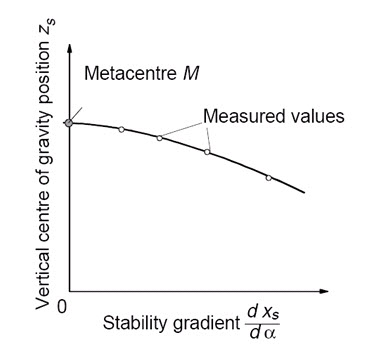Figure 4- Graphical determination of metacenter