Fluid Mechanics 3(2+1)

Lesson-15: CIRCULATION AND VORTICITY

15.1 Circulation, Vorticity and rotation in fluid

• Circulation can be considered as the amount of force that pushes along a closed boundary or path.

• Circulation is the total “push” you get when going along a path, such as a circle.

The circulation, C, about a closed contour in a fluid is defined as the line integral evaluated along the contour of the component of the velocity vector that is locally tangent to the contour.

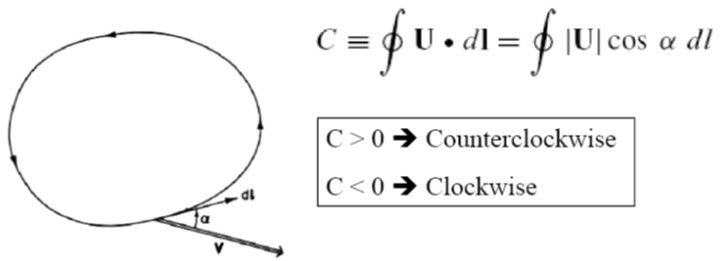
Figure 1: Circulation contour

• One of the difficulties of working with momentum (or velocity) of a parcel in fluid mechanics stems from the pressure forces to which the parcel is subjected, which are continuously changing the parcel’s momentum in complicated ways (since pressure is not fixed, but itself evolves with the flow).

• However, while pressure gradients can change a parcel’s momentum, they cannot change its spin, at least in certain simple situations. Consider two-dimensional, inviscid flow of an incompressible fluid:

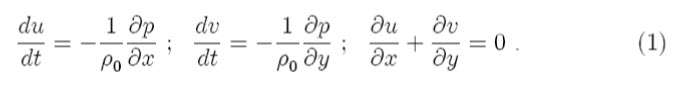
If we take the curl of the momentum equations, the pressure gradient term disappears. So, by taking  of the second of (1) minus  of the first, we get

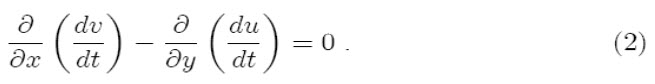
Moreover, a little mathematical juggling [expand the total derivatives, and use the 3rd of (1)] shows that

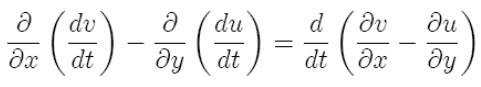
The term inside the bracket on the RHS is the vertical component of the vorticity, de.ned in general by

its vertical component is

Since the flow in this barotropic problem lies within horizontal planes, only the vertical component is nontrivial.

The vorticity is a local measure of the spin of the fluid motion. For example if the fluid (relative to the rotating frame, remember) is in solid body rotation about the origin with angular frequency ω, then (see Fig. 2)

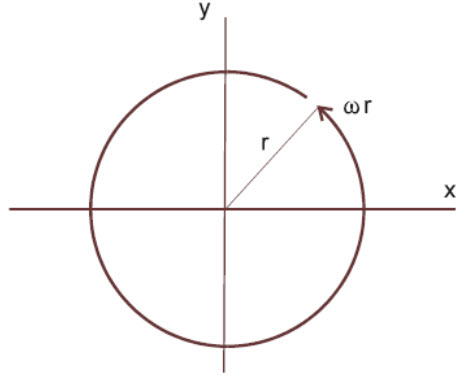
Figure 2: Rotation about the origin; the velocity at position r = (x, y) is U = ω_r.

so the vorticity twice the rotation rate (anticlockwise being positive). [In fact, we can now see that the Coriolis parameter

 

is just the planetary vorticity - the vertical component associated with the planetary  rotation] But vorticity does not have to involve circular flow. A linear shear flow

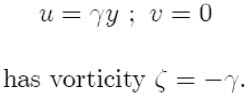
To return to (2), then, we have

This equation states that the time derivative following the motion of the vorticity is (in this simple case) zero. Therefore: In inviscid two-dimensional flow, the vorticity is conserved following the motion.

15.2 Measurement of Rotation

• Circulation and vorticity are the two primary measures of rotation in a fluid.

• Circulation, which is a scalar integral quantity, is a macroscopic measure of rotation for a finite area of the fluid.

• Vorticity, however, is a vector field that gives a microscopic measure of the rotation at any point in the fluid.

Because of shear in the fluid, during flow, an element may not only get translated, but also ‘rotated’. The rotation R is given by :

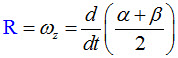
15.3 Solid Body Rotation

• In fluid mechanics, the state when no part of the fluid has motion relative to any other part of the fluid is called 'solid body rotation'.

• If the viscosity of the fluid is zero, the rotation will be zero. It does not mean that the flow is ‘straight’ and not via a circular path; for example, the fluid motion in a centrifuge can be irrotational.

• All real fluids have viscosity and the motion is never truly irrotational with few exceptions (Even in the exception, it doesn’t mean that viscosity is zero, but it means that the problem is definied suitably. Consider the example of an airplane flying in still air. If you take the plane as reference, then the air far away from the plane moves at velocity of –V, but with out feeling viscosity). The equations are useful in obtaining solutions which are good enough in some circumstances. They are also (relatively) easily solvable.

• If a flow is irrotational, the stream function satisfies the Laplace equation. Otherwise, it is given by the Poisson Equation.

• In case the flow is irrotational, it is also called potential flow. The reason is, irrotational flow can be represented as a flow ‘perpendicular’ to lines of equal potentials. (for example, in electricity, there is no current between points of equal potentials. There is flow of current from a point of higher potential to point of lower potential). The fluid flows from a point of higher potential to a point of lower potential.

• Vorticity is the tendency for elements of the fluid to "spin”.

• Vorticity can be related to the amount of “circulation” or "rotation" (or more strictly, the local angular rate of rotation) in a fluid.

15.4 Vorticity

• Vorticity is the tendency for elements of the fluid to "spin”.

• Vorticity can be related to the amount of “circulation” or "rotation" (or more strictly, the local angular rate of rotation) in a fluid.

Definition:

15.6.2 “Depth” of Potential Vorticity

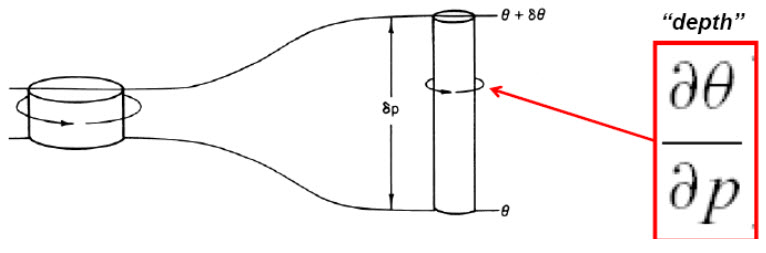
 Figure 2: A cylindrical column of air moving adiabatically conserving potential vortocity

15.5 Stoke’s Theorem

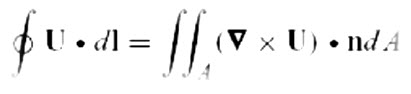
• Stokes’theorem states that the circulation about any closed loop is equal to the integral of the normal component of vorticity over the area enclosed by the contour.

• For a finite area, circulation divided by area gives the average normal component of vorticity in the region.

• Vorticity may thus be regarded as a measure of the local fluid angular velocity of the fluid.

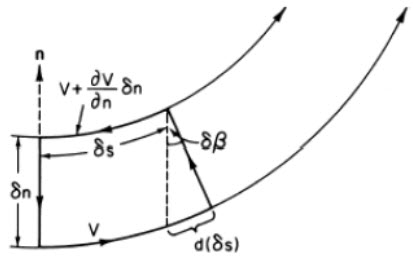
15.6 Vorticity in Natural Coordinate

• Vorticity can be associated with only two broad types of flow configuration.

• It is easier to demonstrate this by considering the vertical component of vorticity in natural coordinates

   

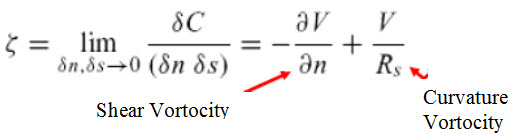
15.7 Ertel’s Potential Vorticity

The quantity P [units: K kg⁻¹ m² s⁻¹] is the isentropic coordinate form of Ertel’s potential vorticity.

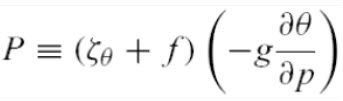
• It is defined with a minus sign so that its value is normally positive in the Northern Hemisphere.

• Potential vorticityis often expressed in the potential vorticity unit (PVU), where 1 PVU = 10⁻⁶ K kg⁻¹ m² s⁻¹.

• Potential vorticity is always in some sense a measure of the ratio of the absolute vorticity to the effective depth of the vortex.

• The effective depth is just the differential distance between potential temperature surfaces measured in pressure units (−∂θ/∂p)

15.8 Depth and Latitude

• The Rossby potential vorticity conservation law indicates that in a barotropic fluid, a change in the depth is dynamically analogous to a change in the Coriolis parameter.

• Therefore, in a barotropic fluid, a decrease of depth with increasing latitude has the same effect on the relative vorticity as the increase of the Coriolis force with latitude.

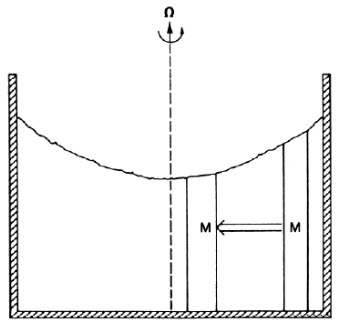
15.9 Velocity Potential

• A velocity potential is used in fluid dynamics when a fluid occupies a simply connected region and is irrotational.

• The potential is related to the velocity components. Equations describing the velocity potential.